2015-04-01
10507
Параллельный колебательный контур – это частотно-избирательная цепь, образованная параллельным соединением индуктивности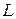 
и емкости 
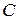. Активные потери контура учитываются сопротивлением 
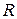, которое подключается последовательно или параллельно (рис. 5.4а,б). Контур широко используется как самостоятельно (полосовой фильтр), так и в составе различных радиотехнических устройств (автогенераторов, модуляторов, преобразователей частоты и др.).
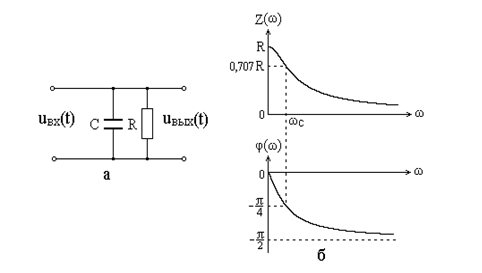
Рис. 5.3. Фильтр нижних частот (а), АЧХ и ФЧХ фильтра (б)
Основные параметры контура и их математические выражения [4,7]:
1. Резонансная частота контура –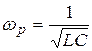 
.
2. Добротность контура (рис. 5.4,а) –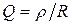 
, добротность контура (рис. 5.4,б) – 
.
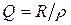3. Волновое сопротивление –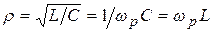 
.
4. Затухание контура –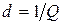 
.
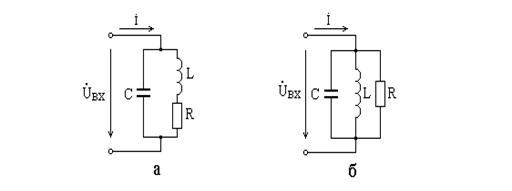
Рис. 5.4. Параллельный колебательный контур с последовательным (а) и
параллельным (б) включением сопротивления потерь
Для описания частотно-избирательных свойств параллельного контура применяют комплексное входное сопротивление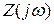 
и частотные коэффициенты передачи по току 
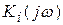и напряжению 
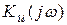– резонансные характеристики контура.
Комплексное входное сопротивление является основной характеристикой контура. Оно равно отношению комплексной амплитуды выходного напряжения к комплексной амплитуде тока в контуре. Определим эту характеристику для контура, изображенного на рис. 5.4,а.
.
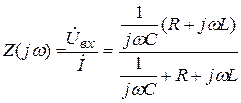Полагаем, что потери в контуре малы. Это позволяет в области резонансной частоты считать, что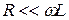 
. Тогда
.
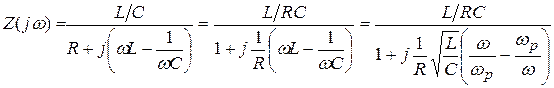Как видно из данной формулы, при резонансе, когда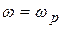 
, входное сопротивление контура носит резистивный характер. Оно называется резонансным сопротивлением и равно
.
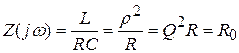Продолжая преобразования формулы для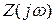 
, получим
,
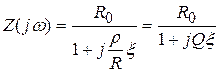где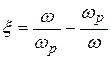 
– частотная расстройка, 
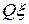– обобщенная расстройка контура.
При малых расстройках в области частот, близких к резонансной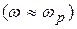 
, можно записать
.
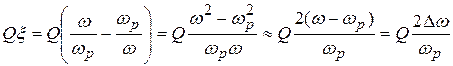Таким образом, комплексное входное сопротивление контура равно
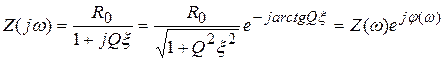. (5.5)
Здесь
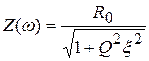– модуль входного сопротивления контура. Зависимость модуля входного сопротивления контура от частоты является амплитудно-частотной характеристикой контура;
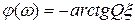– аргумент входного сопротивления контура. Зависимость аргумента входного сопротивления контура от частоты является фазо-частотной характеристикой контура.
Амплитудно-частотная и фазочастотная характеристики параллельного колебательного контура при различных значениях добротности приведены на рис. 5.5.
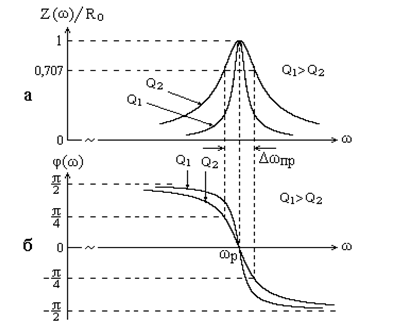
Рис. 5.5. АЧХ (а) и ФЧХ (б) параллельного колебательного контура
Определим полосу пропускания контура на уровне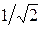 
:
; 
; 
.
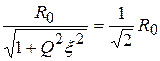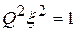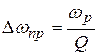Отсюда следует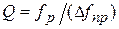 
. Данное определение добротности предоставляет возможность ее экспериментального измерения.
