Дифференцирующая и интегрирующая цепи

На рис. 5.1,а представлена схема линейного четырехполюсника в виде последовательной 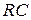-цепи с постоянной времени 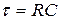. На входе цепи действует напряжение 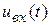, а выходное напряжение 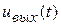может сниматься либо с сопротивления 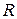, либо с конденсатора 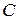. Определим зависимость выходного напряжения от входного для каждого из этих случаев. В соответствии со вторым законом Кирхгофа можно составить уравнение

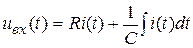, или .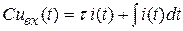

Выполним анализ данного уравнения при большом и малом значениях .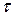

1. Постоянная времени 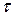– малая величина.

Тогда 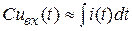или .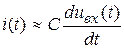

В этом случае выходное напряжение, снимаемое с сопротивления 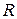, будет равно 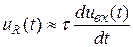. Следовательно, если выходное напряжение снимать с сопротивления, то при малых значениях постоянной времени 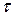последовательная 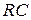-цепь может дифференцировать входной сигнал.

2. Постоянная времени 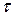– большая величина.

Тогда 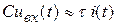или .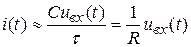

В этом случае выходное напряжение, снимаемое с конденсатора 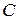, будет равно 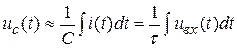. Следовательно, если выходное напряжение снимать с конденсатора, то при больших значениях постоянной времени 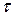последовательная 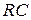-цепь может интегрировать входной сигнал.

Схема дифференцирующей цепи представлена на рис. 5.1,б, интегрирующей цепи – на рис. 5.1,в.

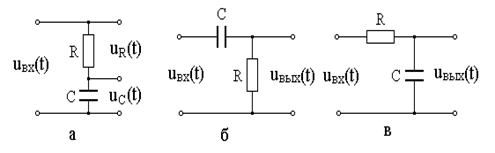
Рис. 5.1. Последовательная 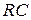-цепь (а), дифференцирующая (б) и

интегрирующая (в) цепи

5.3.1. Дифференцирующая цепь

Определим частотный коэффициент передачи 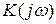дифференцирующей цепи. Комплексная амплитуда тока в цепи определяется законом Ома

.

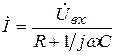Следовательно, комплексная амплитуда выходного напряжения равна

.

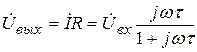Отсюда:

частотный коэффициент передачи 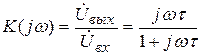; (5.2)

амплитудно-частотная характеристика ;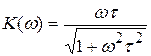

фазочастотная характеристика .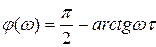

Графики АЧХ и ФЧХ приведены на рис. 5.2,а.

Как следует из графика АЧХ, дифференцирующая цепь является фильтром верхних частот. Определим частоту среза 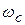на уровне :

; ; .

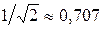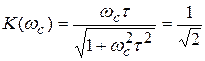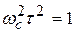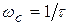Для приближения к точному дифференцированию необходимо, чтобы на всех частотах спектра входного сигнала соблюдалось неравенство 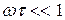. Тогда 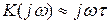– частотная характеристика идеальной дифференцирующей цепи.

5.3.2. Интегрирующая цепь

Определим частотный коэффициент передачи 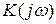интегрирующей цепи. Если комплексная амплитуда тока в цепи равна

,

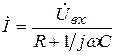то комплексная амплитуда выходного напряжения равна

.

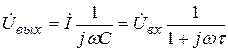Отсюда:

частотный коэффициент передачи 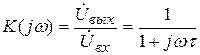; (5.3)

амплитудно-частотная характеристика ;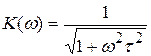

фазочастотная характеристика .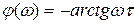

Графики АЧХ и ФЧХ приведены на рис. 5.2,б.

Как следует из графика АЧХ, интегрирующая цепь является фильтром нижних частот. Частота среза также равна .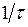

Для приближения к точному интегрированию необходимо, чтобы на всех частотах спектра входного сигнала соблюдалось неравенство 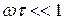. Тогда 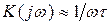– частотная характеристика идеальной интегрирующей цепи.

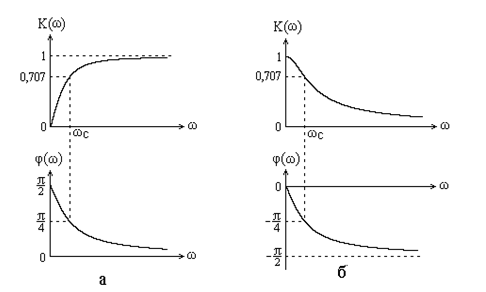
Рис. 5.2. АЧХ и ФЧХ дифференцирующей (а) и интегрирующей (б)

цепей