Спектр непериодического сигнала (спектральная плотность) определяется путем вычисления прямого преобразования Фурье
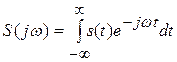 . (6.1)
. (6.1)
В свою очередь обратное преобразование Фурье позволяет определить сигнал по его спектру, т.е.
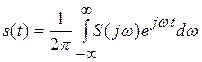 . (6.2)
. (6.2)
Как видно из данного выражения, сигнал 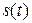 представляется в виде суммы бесконечно большого числа незатухающих и бесконечно близких по частоте гармонических колебаний с бесконечно малыми комплексными амплитудами, равными
представляется в виде суммы бесконечно большого числа незатухающих и бесконечно близких по частоте гармонических колебаний с бесконечно малыми комплексными амплитудами, равными 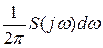 . Это дает возможность использовать обычные методы расчета установившихся режимов.
. Это дает возможность использовать обычные методы расчета установившихся режимов.
Применительно к решаемой задаче, каждая из таких гармонических составляющих входного сигнала обусловит соответствующую гармоническую составляющую выходного сигнала с комплексной амплитудой, равной
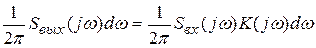 .
.
На основании этого можно записать выражение для спектральной плотности выходного сигнала, которое является фундаментальным для рассматриваемого метода анализа линейных цепей,
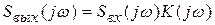 . (6.3)
. (6.3)
Таким образом, спектральная плотность выходного сигнала равна произведению спектральной плотности входного сигнала на частотную характеристику цепи.
Выходной сигнал находится с помощью обратного преобразования Фурье, реализующего суммирование бесконечно большого числа его гармонических составляющих:
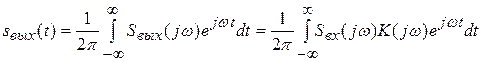 . (6.4)
. (6.4)
Можно предложить следующую последовательность анализа линейных цепей спектральным методом.
1. Определение спектральной плотности 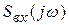 входного сигнала по формуле (6.1).
входного сигнала по формуле (6.1).
2. Определение частотной характеристики цепи одним из известных методов (уравнений Кирхгофа, контурных токов, узловых потенциалов, наложения, из дифференциального уравнения цепи и др.).
3. Расчет спектральной плотности 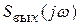 выходного сигнала по формуле (6.3).
выходного сигнала по формуле (6.3).
4. Определение выходного сигнала по формуле (6.4).
В некоторых случаях целесообразно использовать операторный метод анализа цепей, основанный на преобразованиях Лапласа. При этом функции действительной переменной 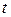 преобразуются в функции комплексной частоты, т.е. переменной
преобразуются в функции комплексной частоты, т.е. переменной 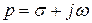 . Для этого используются преобразования Лапласа:
. Для этого используются преобразования Лапласа:
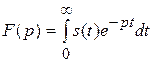 и
и 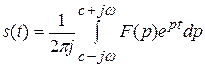 .
.
Функцию 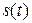 называют оригиналом, а функцию
называют оригиналом, а функцию 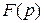 – изображением оригинала по Лапласу или просто изображением. Как видно из данных выражений, преобразования Фурье могут быть получены из преобразований Лапласа простой заменой
– изображением оригинала по Лапласу или просто изображением. Как видно из данных выражений, преобразования Фурье могут быть получены из преобразований Лапласа простой заменой 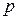 на
на 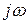 с соответствующим изменением пределов интегрирования. Преобразования Лапласа являются обобщениями преобразований Фурье, поэтому они обладают всеми свойствами, которые характерны для преобразований Фурье.
с соответствующим изменением пределов интегрирования. Преобразования Лапласа являются обобщениями преобразований Фурье, поэтому они обладают всеми свойствами, которые характерны для преобразований Фурье.
Частотная характеристика цепи в операторной форме получается простой заменой переменной 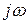 на комплексную переменную
на комплексную переменную 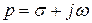 , т.е.
, т.е.
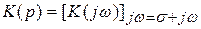 .
.
Выражение (6.3.) для спектра выходного сигнала цепи будет иметь вид
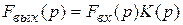 .
.
Операторный метод позволяет анализировать более широкий класс сигналов. В частности, этому методу доступны сигналы, описываемые функциями, которые не удовлетворяют условию абсолютной интегрируемости. В литературе [1,2] имеются таблицы изображений и оригиналов, облегчающие применение операторного метода.
Спектральный и операторный методы анализа линейных цепей успешно применяются для решения многих вопросов теории связи и управления. При этом удается обойти серьезные трудности, связанные с вычислением корней характеристического уравнения систем высокого порядка. Частотный метод имеет важное значение особенно в тех случаях, когда уравнение системы вообще неизвестно и когда можно ограничиться качественным исследованием динамических свойств систем.
6.2.3. Временной метод
Временной метод (метод интеграла наложения, метод интеграла Дюамеля) основан на использовании импульсной 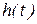 характеристики цепи, т.е. характеристики цепи во временной области. Импульсная характеристика – это реакция цепи на
характеристики цепи, т.е. характеристики цепи во временной области. Импульсная характеристика – это реакция цепи на 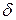 -функцию. Такой функцией описывается модель сигнала, имеющего бесконечно большую амплитуду, нулевую длительность и площадь, равную 1.
-функцию. Такой функцией описывается модель сигнала, имеющего бесконечно большую амплитуду, нулевую длительность и площадь, равную 1.
Представим входной сигнал 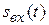 сложной формы в виде совокупности прямоугольных импульсов одинаковой и достаточно малой длительности
сложной формы в виде совокупности прямоугольных импульсов одинаковой и достаточно малой длительности 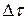 (рис. 6.2).
(рис. 6.2).
Реакция цепи в моменты времени 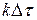 ,
, 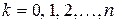 на каждый из этих импульсов (если бы площади их были равны единице) – есть импульсная характеристика
на каждый из этих импульсов (если бы площади их были равны единице) – есть импульсная характеристика 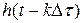 . Но так как площади импульсов равны
. Но так как площади импульсов равны 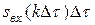 , то
, то
реакция цепи равна 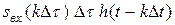 . В свою очередь выходной сигнал в некоторый момент времени
. В свою очередь выходной сигнал в некоторый момент времени 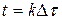 будет равен сумме реакций цепи на импульсы в интервале
будет равен сумме реакций цепи на импульсы в интервале 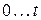 , т.е.
, т.е.
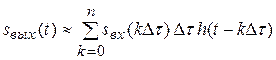 .
.
При 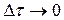 суммирование сводится к операции интегрирования по переменной
суммирование сводится к операции интегрирования по переменной 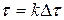 :
:
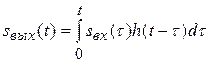 .
.
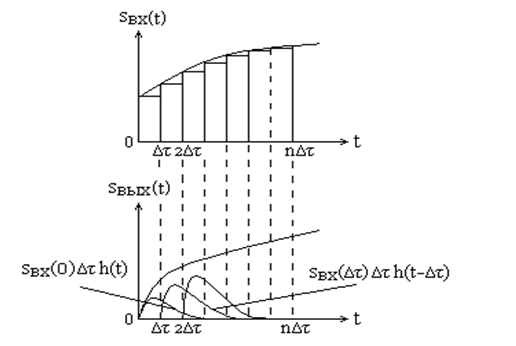
Рис. 6.2. Свертка сигнала с импульсной характеристикой
Таким образом, значения выходного сигнала линейной цепи в любой момент времени являются результатом взвешенного суммирования мгновенных значений входного сигнала. Весовая функция – это импульсная характеристика цепи.
Учитывая, что для реальных цепей 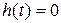 при
при 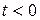 , можно записать
, можно записать
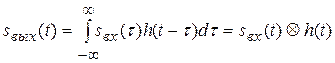 .
.
Полученное выражение для 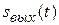 представляет собой интеграл наложения, или интеграл Дюамеля. В математике полученное выражение называют сверткой двух функций. Таким образом, выходной сигнал линейной цепи равен свертке входного сигнала и импульсной характеристики цепи.
представляет собой интеграл наложения, или интеграл Дюамеля. В математике полученное выражение называют сверткой двух функций. Таким образом, выходной сигнал линейной цепи равен свертке входного сигнала и импульсной характеристики цепи.
Иногда используют другую форму записи интеграла Дюамеля, которую можно получить путем замены переменной 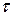 на
на 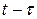 ,
,
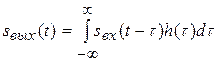 .
.
Заметим, что интеграл Дюамеля можно получить из формулы 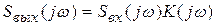 , на которой основан спектральный метод анализа цепей. Для этого воспользуемся свойствами преобразования Фурье и связью между частотной и импульсной характеристиками цепи, имея в виду, что частотная характеристика
, на которой основан спектральный метод анализа цепей. Для этого воспользуемся свойствами преобразования Фурье и связью между частотной и импульсной характеристиками цепи, имея в виду, что частотная характеристика 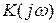 цепи является по существу спектральной плотностью ее импульсной характеристики
цепи является по существу спектральной плотностью ее импульсной характеристики 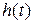 .
.
Из свойств преобразования Фурье известно, что произведению двух спектров соответствует свертка сигналов, соответствующих данным спектрам. Таким образом, можно записать
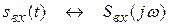 ;
;
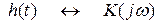
 |
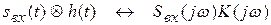 .
.
Следовательно, спектру 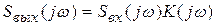 соответствует сигнал
соответствует сигнал
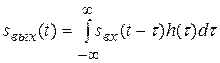 ,
,
что и требовалось доказать.
 2015-04-01
2015-04-01 1673
1673
