Свойства определенных интегралов

1. Постоянный множитель можно вынести за знак интеграла: .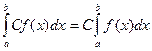

2. Интеграл суммы (разности) равен сумме (разности) интегралов: .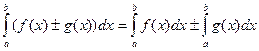

3. При равных пределах интегрирования интеграл равен нулю: .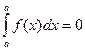

4. При перестановке пределов интегрирования интеграл меняет знак: .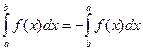

5. Интеграл можно представить в виде суммы двух интегралов 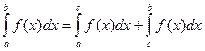, где с новый предел интегрирования, который может находиться как в интервале (a, b), так и вне этого интервала.