Интегрирование по частям. Интегрированием по частям называется интегрирование по формуле

Интегрированием по частям называется интегрирование по формуле:

.

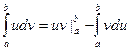@ Задача 3. Вычислить .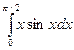

Решение: .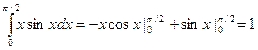

Несобственные интегралы

Определенный интеграл с одним или двумя бесконечными пределами интегрирования называется несобственным интегралом первого типа.

þ Обозначения: , , .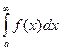

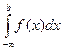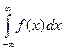@ Задача 4. Вычислить .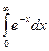

Решение: .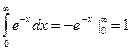

Известным примером несобственного интеграла является интеграл Эйлера-Пуассона: .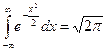

Определенный интеграл с функцией f(x), имеющий разрыв на отрезке [ a; b ], называется несобственным интегралом второго типа.

Пример: Подынтегральная функция интеграла 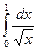в точке x = 0 имеет разрыв.