Приближенное вычисление

На практике часто встречаются интегралы, которые не выражаются через элементарные функции. В этом случае интегралы можно взять приближенными методами: по формулам прямоугольников, трапеций и Симпсона.

По формуле трапеций интеграл вычисляется как

,

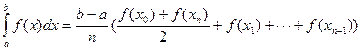где 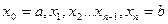- точки отрезка [ a; b ].

Предельная погрешность формулы трапеций составляет 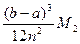, где M ₂– наибольшее значение | f²(x)| в промежутке [ a; b ].

Пример. .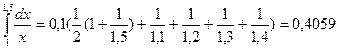

По формуле Симпсона (параболических трапеций) интеграл вычисляется как

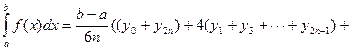
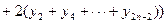
Предельная погрешность формулы Симпсона составляет 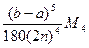, где M ₄– наибольшее значение | f ^IV (x)| в промежутке [ a; b ].