Решение метрических задач с помощью преобразования комплексного чертежа

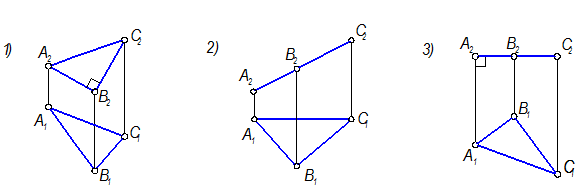
Как вы думаете?

На каком из чертежей уже присутствует натуральная величина треугольника АВС?

Преобразование комплексного чертежа часто используется при решении метрических задач. В этом случае конечной целью преобразования чертежа является получение такой проекции оригинала, на которой можно было бы видеть в натуральную величину геометрический элемент, связанный с искомой метрической характеристикой.

Такое положение оригинала относительно некоторой плоскости проекций, при котором по проекции можно непосредственно определить нужную метрическую характеристику, называется решающим положением оригинала.

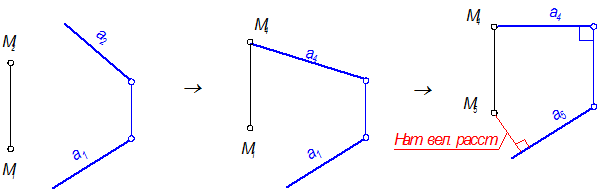
1. Например: Заданы две параллельные прямые а и b (рис. 4-52). Требуется определить расстояние между ними.

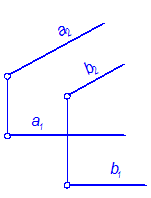
Рис. 4-52

В этом случае решающим положением параллельных прямых будет положение перпендикулярности к плоскости проекций. Так как прямые а и b являются фронталями, то, чтобы поставить их в проецирующее положение, потребуется только одна замена (то есть, нужно решить вторую задачу преобразования комплексного чертежа). Для решения выбираем способ замены плоскостей проекций.

Алгоритм решения (рис. 4-53):

1. П₁ Þ П₄,

П₄ ^ П₂; П₄ ^ а, b Þ x₂₄ ^ a₂b₂

2. Расстояние х₂₄а₄ = х₁₂а₁; х₂₄b₄ = х₁₂b₁.

3. a₄, b₄ - точки.

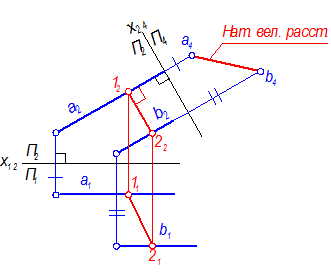
Рис. 4-53

Таким образом, прямые а и b на П₄ проецируются в точки, и расстояние между а₄ и b₄ определяет расстояние между прямыми а и b. Возвращаем это расстояние в систему П₂ – П₁ (1₂2₂ -1₁2₁).

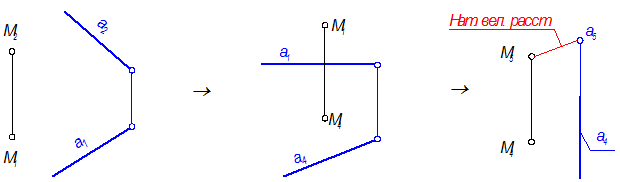
2. Например, для нахождения натурального вида плоской фигуры решающим положением является такое, при котором плоскость, в которой расположена эта фигура, параллельна какой-нибудь плоскости проекций (см. четвёртую задачу преобразования комплексного чертежа, стр. М4-16, рис. 4-40б).

Следует отметить, что для решения ряда задач данный оригинал может иметь несколько решающих положений. Так, например, в задаче на определение расстояния от точки до прямой легко можно увидеть два решающих положения:

1. Когда данная прямая будет перпендикулярна какой-нибудь плоскости проекций (решается вторая основная задача преобразования комплексного чертежа) (рис. 4-54).

а)

б)

в)

Рис. 4-54

2. Когда плоскость, определяемая заданными прямой и точкой, займёт положение, параллельное какой-нибудь плоскости проекций (решается четвёртая задача преобразования комплексного чертежа) (рис. 4-55).

а)

б)

в)

Рис. 4-55

Несмотря на огромное разнообразие метрических задач, можно записать единый алгоритм их решения с использованием преобразования комплексного чертежа:

1. Устанавливают наличие метрической характеристики в задаче.
2. Определяют носителя этой метрической характеристики.
3. Выбирают "решающее положение" оригинала, при котором по проекции можно сразу определить натуральную величину геометрического элемента, связанного с метрической характеристикой. Решающее положение оригинала определяется выбором одной из четырёх задач преобразования комплексного чертежа.
4. Выбирают рациональный способ преобразования.

Всё вышеизложенное рассмотрим на примере конкретной конструктивной задачи.

Задача: Построить проекции равностороннего треугольника АВС, принадлежащего плоскости Г(h Ç f), если его сторона АВ задана (рис. 4-56).

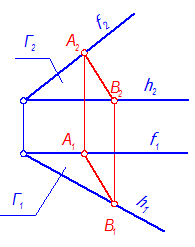
Рис. 4-56

Алгоритм:

1. Чтобы построить проекции треугольника АВС, необходимо сначала определить его истинный вид. В этом случае решающим положением оригинала (DАВС) является то, при котором плоскость треугольника параллельна плоскости проекций. Для этого плоскость Г(h Ç f) нужно поставить в положение плоскости уровня.

2. Чтобы плоскость Г поставить в положение плоскости уровня, требуется решить четвёртую задачу преобразования комплексного чертежа. Выбираем способ замены плоскостей проекций. Для решения четвёртой задачи требуется выполнить две замены.

3. Фиксируем систему П₁ –П₂, то есть, проводим х₁₂ (рис. 4-57).

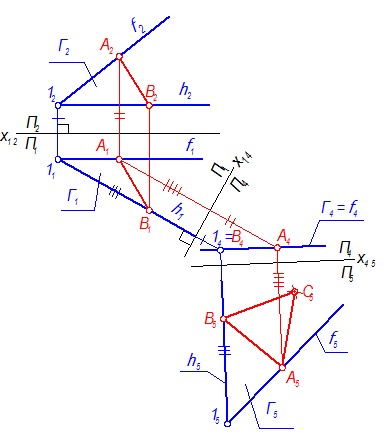
Рис. 4-57

4. Меняем П₂ на П₄.

П₄ ^ П₁; П₄ ^ Г; П₄ ^ h Þ x₁₄h₁

Так как плоскость Г на П₄ спроецируется в прямую линию, то для её построения требуется всего 2 точки: Расстояние х₁₄1₄ = х₁₂1₂, х₁₄А₄ = х₁₂А₂. Г₄ - главная проекция.

5. Меняем П₁ на П₅.

П₅ ^ П₄; П || Г Þ x₄₅ || Г

Расстояние х₄₅1₅ = х₁₄1₁, х₄₅А₅ = х₁₄А₁.

6. В системе П₄ – П₅ плоскость Г - плоскость уровня, поэтому отрезок А₅В₅ - натуральная величина АВ, и треугольник АВС спроецируется на П₅ в натуральную величину. Для его построения из точек А₅ и В₅ откладываем отрезки, равные А₅В₅, и получаем точку С₅. Проекция А₅В₅С₅ - натуральная величина равностороннего треугольника АВС.

7. Возвращаем точку С в систему П₁ – П₂ в обратном порядке (рис. 4-58).

Сначала находим С₄ на Г₄, проведя линию связи от С₅ перпендикулярно х₄₅.

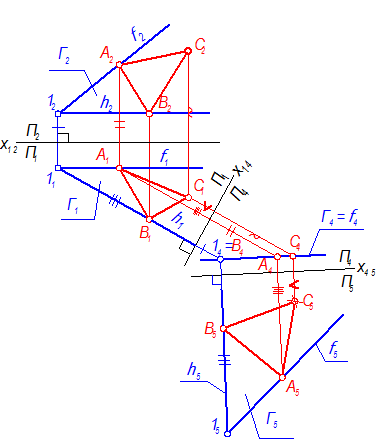
Рис. 4-58

8. От С₄ проводим линию связи в системе П₁ – П₄ и откладываем расстояние х₁₄С₁ = х₄₅С₅.

9. От С₁ проводим линию связи в системе П₁ – П₂ и откладываем расстояние х₁₂С₂ = х₁₄С₄.

10. Мы построили проекции равностороннего DАВС, принадлежащего плоскости Г(h Ç f).

Общая схема решения показана на рис. 4-59:

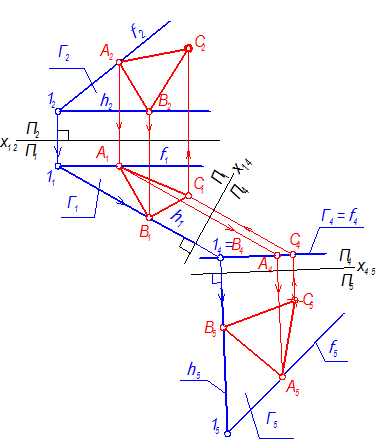
Рис. 4-59

Задача: Определить расстояние между прямыми а и b (рис. 4-60).

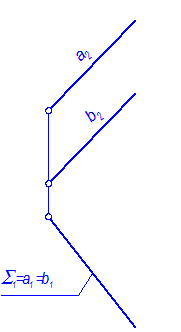
Рис. 4-60

Алгоритм:

1. В данной задаче параллельными прямыми а и b задана горизонтально проецирующая плоскость S(а || b). Чтобы расстояние между прямыми оказалось на чертеже в натуральную величину, решающим положением оригинала является такое, при котором плоскость S стала бы плоскостью уровня. Для этого необходимо решить четвёртую задачу преобразования комплексного чертежа.

2. Для преобразования выбираем способ вращения вокруг проецирующей оси. Так как плоскость S проецирующая, то для достижения цели достаточно одного вращения.

3. Выбираем ось вращения i так, чтобы она была горизонтально проецирующей (рис. 4-61а).

4. Радиус вращения R = i₁1₁

5. Вращаем проекцию плоскости S вокруг оси i₁ до момента, когда она станет перпендикулярной линиям связи, и займёт положение S₁' (рис. 4-61б).

6. Фронтальные проекции точек 1₂ и 2₂ совершат движение вправо по прямым, перпендикулярным линиям связи, и займут положение 1₂' и 2₂'.

7. Прямые а₂' и b₂' - прямые уровня и расстояние между ними КР - натуральная величина расстояния между прямыми а и b (рис. 4-61в).

8. Возвращаем расстояние на П₂ в обратном порядке (рис. 4-61г) - получаем К₂Р₂.

а)

б)

в)

г)

Рис. 4-61