Решение позиционных задач с помощью преобразования комплексного чертежа

Как вы думаете?

В каком случае проще решается задача на пересечение конуса Г с плоскостью?

Многие позиционные задачи, главным образом, задачи на пересечение поверхностей с прямыми или плоскостями общего положения, удобно решать с помощью преобразования комплексного чертежа. В этом случае конечной целью преобразования является получение такой проекции оригинала, при которой участвующие в пересечении прямая или плоскость находятся в частном положении. Тогда в новом положении решение задачи значительно упрощается. При необходимости проекции общего элемента возвращают в исходный чертёж в обратном порядке.

Рассмотрим вышесказанное на конкретном примере.

Задача: Найти точки пересечения сферы с прямой а (рис. 4-62).

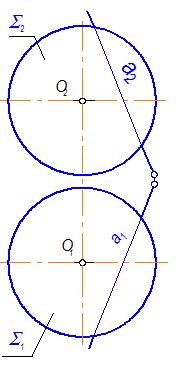
Рис. 4-62

Алгоритм:

1. Выбираем решающее положение оригинала. Оно должно быть таким, чтобы прямая а и окружность b на сфере S (рис. 4-63), лежащие в одной плоскости, оказались бы в натуральную величину. Для этого плоскость окружности Г должна быть плоскостью уровня. Выбираем способ замены плоскостей проекций.

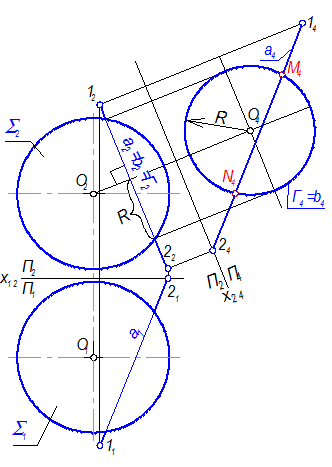
Рис. 4-63

2. Так как плоскость Г - проецирующая, то требуется одна замена.

3. Решаем четвёртую задачу преобразования комплексного чертежа. Фиксируем систему П₁ – П₂, проводим базу х₁₂.

4. Меняем П₁ на П₄. П₄ ^ П₂, П || Г Þ х₂₄ || Г₂.

5. От точки О₂ проводим линию связи в системе П₂ – П₄ перпендикулярно Г₂ и откладываем расстояние х₂₄О₄ = х₁₂О₁. Получили центр окружности b, и проводим окружность b₄ радиусом R.

6. Проецируем прямую а на П₄. Для этого на ней отметим точки 1 и 2 и откладываем расстояния: х₂₄1₄ = х₁₂1₁, х₂₄2₄ = х₁₂2₁. Получили а₄.

7. Там, где а₄ пересечётся с b₄, будут точки M₄ и N₄.

8. Возвращаем точки M и N в систему П₂ – П₁ в обратном порядке по принадлежности прямой а (рис. 4-64).

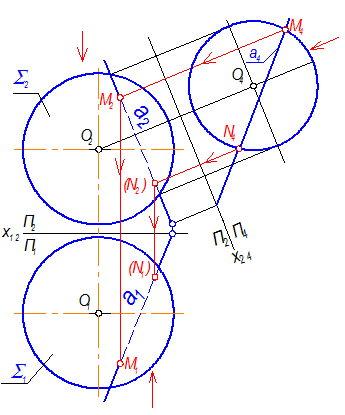
Рис. 4-64

9. Видимость точек можно определить, например, так, как обычно определяют её на сфере: точка М₂ расположена выше экватора Þ М₁ - видимая, точка N₂ - ниже экватора Þ N₂ - невидимая. Точка М₁ расположена ближе плоскости фронтального меридиана Þ М₂ - видимая, точка N₁ - дальше плоскости фронтального меридиана Þ N₂ - невидимая.

Выводы:

1. Преобразование комплексного чертежа значительно упрощает решение метрических и позиционных задач.

2. При решении конструктивных задач важным моментом является выбор решающего положения оригинала.

3. Несмотря на разнообразие конструктивных задач, существует единый алгоритм их решения.

Контрольные вопросы

1. С какой целью применяется преобразование комплексного чертежа?
2. Как формулируются четыре основные задачи преобразования эпюра Монжа?
3. Изменяются ли эти формулировки в разных способах преобразования эпюра Монжа?
4. Сформулируйте основные правила замены плоскостей проекций.
5. Почему задачи 1-2, 3-4 решаются на одном чертеже? Как можно это прокомментировать?
6. Какими элементами в способе вращения можно распоряжаться произвольно?
7. Что происходит с точкой, лежащей на оси вращения, при вращении геометрических фигур?
8. Как вращаются остальные точки?
9. Можно ли одним вращением прямую общего положения поставить в проецирующее положение?
10. Как выбирают новую плоскость проекций относительно остающейся?
11. Как преобразовать плоскость общего положения в проецирующую?
12. Что называется "решающим" положением оригинала?