Определение 8. Однородные линейные алгебраические системы составлены из уравнений, у которых правые части раны нулю:
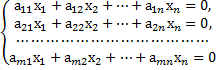
A =  – Матрица системы,
– Матрица системы,
Х = 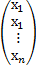 – матрица-столбец неизвестных,
– матрица-столбец неизвестных,
Тогда матричная форма записи системы будет: АХ=0
Однородная система всегда совместна, так как имеет нулевое решение  =0,
=0,  =0,…,
=0,…, 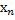 =0 или Х=0. Для существования ненулевого решения однородной системы необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных, т.е. чтобы r= r(A)
=0 или Х=0. Для существования ненулевого решения однородной системы необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных, т.е. чтобы r= r(A) 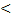 n (при m=n это условие означает, что detA=0).
n (при m=n это условие означает, что detA=0).
Определение 9. Пусть Q 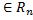 - множество всех решений однородной системы. Всякий базис в множестве Q состоит из n-r векторов
- множество всех решений однородной системы. Всякий базис в множестве Q состоит из n-r векторов 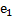 ,
, 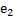 ,…,
,…, 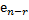 .Соответствующая ему в каноническом базисе система вектор-столбцов
.Соответствующая ему в каноническом базисе система вектор-столбцов 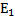 ,
, 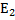 , …,
, …, 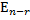 называется фундаментальной системой решений.
называется фундаментальной системой решений.
Общее решение однородной системы имеет вид:
Х= 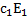 +
+ 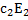 +…+
+…+ 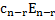 , где
, где 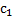 ,
, 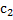 ,…,
,…, 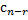 –произвольные постоянные.
–произвольные постоянные.
Базисные решения 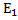 ,
, 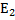 ,…,
,…, 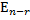 могут быть получены с помощью элементарных преобразований матрицы системы приведением ее к ступенчатому виду, если независимым неизвестным придавать поочередно значение 1, полагая остальные равным нулю. Если задана неоднородная система АХ=b, то ее общее решение может быть найдено как сумма общего решения соответствующей однородной системы АХ=0 и произвольного частного решения неоднородной системы.
могут быть получены с помощью элементарных преобразований матрицы системы приведением ее к ступенчатому виду, если независимым неизвестным придавать поочередно значение 1, полагая остальные равным нулю. Если задана неоднородная система АХ=b, то ее общее решение может быть найдено как сумма общего решения соответствующей однородной системы АХ=0 и произвольного частного решения неоднородной системы.
Пример 4. Найти фундаментальную систему решений однородной системы уравнений.
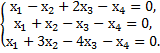
Решение.
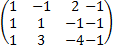 (2)-(1) (3)-(1)
(2)-(1) (3)-(1) 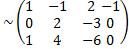 (3)-2(2)
(3)-2(2) 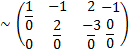 2(1)
2(1) 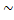
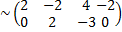 (1)+(2)
(1)+(2) 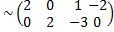 .
.
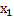 -з
-з 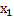 -з
-з
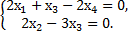 Общее решение системы
Общее решение системы
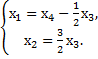 Найдем фундаментальную систему решений.
Найдем фундаментальную систему решений.
Так как r(A)=2,n=4, то независимых неизвестных будет n-r=2 т.е. фундаментальная система будет состоять из двух векторов.
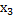
| 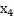
| 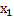
| 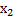
| |
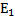
| - 
| 
| ||
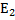
|
Таким образом, 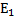 =
= 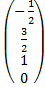 ,
, 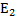 =
= 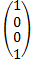 -образуют фундаментальную систему решений. Общее решение системы есть Х=
-образуют фундаментальную систему решений. Общее решение системы есть Х=  +
+ 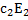 .
.
Ответ: векторы 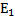 ,
, 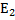 образуют фундаментальную систему решений, общее решение системы будет Х=
образуют фундаментальную систему решений, общее решение системы будет Х= 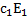 +
+ 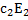 ,
, 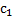 ,
, 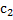 –произвольные постоянные,
–произвольные постоянные, 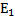 =
= 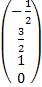 ,
, 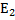 =
= 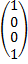 .
.
Задания для самостоятельного решения.
1. Решить систему уравнений по формулам Крамера и матричным способом.
а) 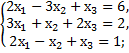 б)
б) 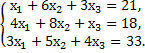
2. Решить систему уравнений по формулам Крамера и матричным способом.
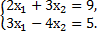
3. Решить системы уравнений:
а) 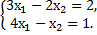 б)
б) 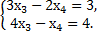 в)
в) 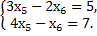
Указание. Записать все три системы в виде одного матричного уравнения.
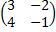 ·
· 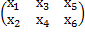 =
= 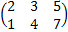 , т.е. в виде АХ=В, или Х=
, т.е. в виде АХ=В, или Х= 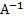 ·В.
·В.
4. Является система векторов линейно зависимой или нет?
a) 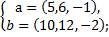 б)
б) 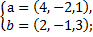 в)
в) 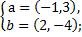 г)
г) 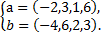
5. Проверить, что система векторов 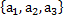 образует базис в
образует базис в 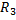 , и найти разложение вектораd в этом базисе, если:
, и найти разложение вектораd в этом базисе, если:
а) 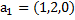 ,
, 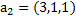 ,
, 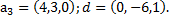
б) 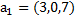 ,
, 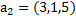 ,
, 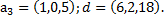
в) 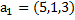 ,
, 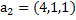 ,
, 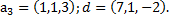
6. Найти методом Гаусса все решения системы
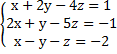
7. Исследовать систему уравнений с помощью теоремы Кронекера-Капелли.
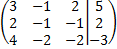 .
.
8. Исследовать системы уравнений с помощью теоремы Кронекера-Капелли и решить их.
а) 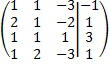 ; б)
; б)  ;
;
в) 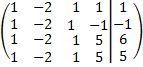 ; г)
; г) 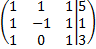 ;
;
д) 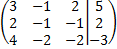 .
.
9. Исследовать совместимость и найти общее решение следующих систем:
а) 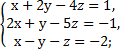 б)
б) 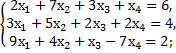
в) 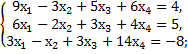
г) 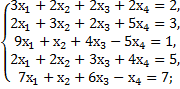 д)
д) 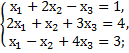
е) 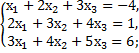 ж)
ж) 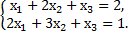
10. Найти фундаментальную систему решений и общее решение следующих систем:
а) 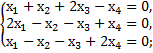
б) 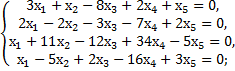
в) 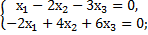 г)
г) 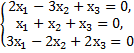
д) 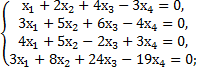
11. Найти общие решения неоднородных систем, используя фундаментальную систему решений соответствующих однородных:
а) 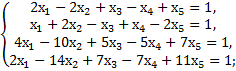
б) 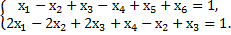
 2015-04-01
2015-04-01 660
660








