След матрицы

Следом квадратной матрицы 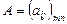, называется сумма её диагональных элементов, то есть число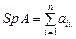

Справедливы следующие утверждения:

1)

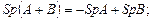
2)

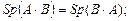
3) Если А и B подобные матрицы, т.е. 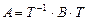, то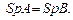

Утверждение 1 доказывается непосредственным вычислением. Докажем свойство 2:

,

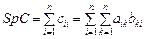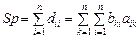
Эти суммы равны, так как отличаются только порядком слагаемых. Докажем свойство 3:

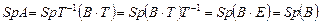
Пример. Найти след матрицы:

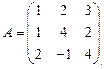
Найдем след матрицы А вручную. .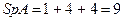

Найдем след матрицы А с помощью Mathcad:

1. Задаем системную переменную

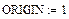
2. Задаем матрицу

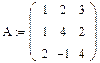
3. Находим след матрицы А как сумму её диагональных элементов

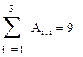
4. Данная операция также может быть организована в виде встроенной функции tr():

tr (A) – след квадратной матрицы А

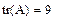
Пример.

Подобны ли матрицы 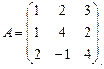и ?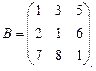

Ответ. Нет, так как 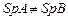, но следует учитывать, что если бы след у них был одинаковым, утверждать о подобности матриц все равно было бы нельзя.