Матрица 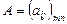 называется симметрической, если
называется симметрической, если 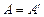 или
или 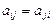 .
.
Матрица 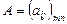 называется кососимметрической, если
называется кососимметрической, если 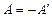 или
или 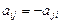 .
.
Легко видеть, что для кососимметрической матрицы 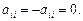
Пример. 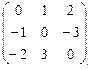
Любая матрица может быть представлена как сумма симметрической и кососимметрической.
Действительно: 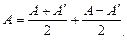
Матрица 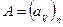 называется ортогональной, если
называется ортогональной, если 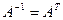 , из определения следует, что для ортогональной матрицы А:
, из определения следует, что для ортогональной матрицы А: 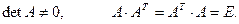
Можно доказать, что матрица А ортогональна тогда и только тогда, когда столбцы (строки) матрицы образуют ортонормированную систему векторов.
Если А – ортогональная матрица, то система линейных уравнений 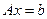 решается мгновенно.
решается мгновенно.
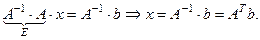
Пример.Решить систему
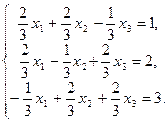
Матрица  ортогональна (проверьте!)
ортогональна (проверьте!)
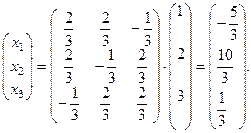

Ответ. 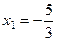 ,
, 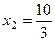 ,
, 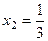 .
.
 2015-04-01
2015-04-01 883
883








