Пусть дана матрица:
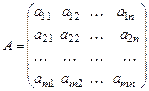
Минором k -го порядка матрицы А назовем определитель матрицы с элементами, стоящими на пересечении выбранных k строк и k столбцов.
Минор обозначается так:
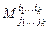 ,
,
где i1, i2,... ik - номера выделенных строк;
j1, j2,..., jk - номера выделенных столбцов.
Пример:
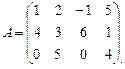
1. 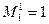 .
.
2. Выпишем какой-нибудь минор второго порядка. Для этого выберем, например, 1-ю и 3-ю строки, 2-й и 4-й столбец.
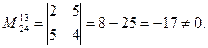
3. Найдем какой-нибудь минор 3-го порядка. Для этого нужно выбрать все строки и какие-нибудь три столбца, например 2-й, 3-й и 4-й.
Получим минор:
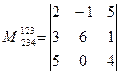
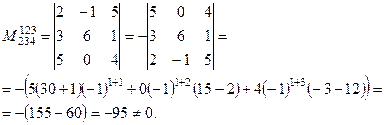 *знак «–» означает, что 2 строки в определителе переставлены местами.
*знак «–» означает, что 2 строки в определителе переставлены местами.
Минор называется невырожденным, если его определитель не равен нулю.
В нашем примере миноры невырожденные.
Рангом матрицы А называется наивысший порядок невырожденных миноров матрицы (обозначается rang A).
В нашем примере rang A=3, так как мы нашли невырожденный минор третьего порядка, а миноров четвертого порядка у нашей матрицы нет. Любой невырожденный минор порядка rang A называется базисным.
Для базисного минора выполняются следующие правила:
1) Столбцы, входящие в базисный минор, линейно независимы, так как в противном случае какой-то столбец из нашего минора линейно выражался бы через остальные и тогда определитель минора равнялся бы нулю.
2) Столбцы, не входящие в базисный минор, линейно выражаются через базисы.
Эти утверждения справедливы и для строк матрицы.
Существуют разные способы определения ранга матрицы. Рассмотрим метод Гаусса определения ранга. Для этого рассмотрим элементарные преобразования:
1) перестановку строк (столбцов) матрицы;
2) умножение строк (столбцов) на константу ¹ 0;
3) прибавление к i -той строке (столбцу) j-той строки (столбца), умноженной (умноженного) на некоторое число;
4) вычеркивание из матрицы нулевых строк (столбцов).
Все эти преобразования не меняют ранга матрицы.
Метод Гаусса нахождения ранга матрицы заключается в следующем. С помощью элементарных преобразований приводим матрицу А к виду:
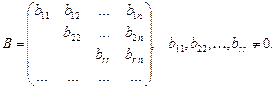
rang B = r.
Базисный минор – это минор
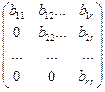 , rang A = rang B = 2.
, rang A = rang B = 2.
Пример. Найти ранг матрицы 
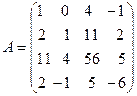
Решение.
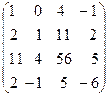
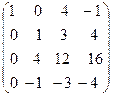
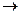
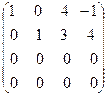
rang A=2.
Рассмотрим систему уравнений 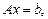 система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу расширенной матрицы, т.е.
система совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу расширенной матрицы, т.е.
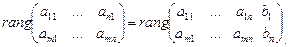
Можно доказать, что
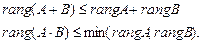
Пример. Найти ранг и базисный минор матрицы А с помощью Mathcad.
1. Задаем системную переменную, вводящую нумерацию элементов массива с единицы.
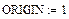
2. Задаем элементы матрицы А.
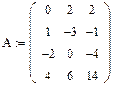
3. Задаем ранжированные переменные, определяющие изменение порядковых номеров строк (i) и столбцов (j) матрицы А.
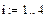
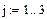
4. Осуществляем линейные операции с элементами строк и столбцов матрицы А согласно методу Гаусса.
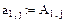
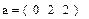
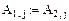
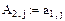
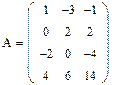
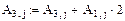
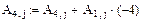
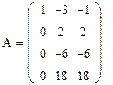
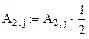
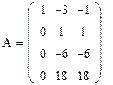
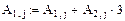
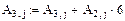
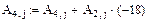
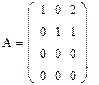
5. Дальнейшее преобразование бессмысленно. Ранг преобразованной матрицы А=2.
6. Осуществим проверку полученного результата с помощью встроенной функции MathCad rank().
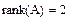
7. Базисный минор матрицы А содержит 2 строки и 2 столбца. Его определитель не равен нулю.
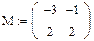
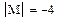
 2015-04-01
2015-04-01 1420
1420
