Свойства тензоров второго ранга 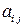 эквивалентны свойствам квадратной матрицы
эквивалентны свойствам квадратной матрицы 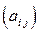 , построенной из компонент тензора.
, построенной из компонент тензора.
Тензор второго ранга 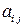 называется симметричным, если для любых индексов i и j выполняется равенство:
называется симметричным, если для любых индексов i и j выполняется равенство: 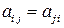 .
.
Тензор второго ранга 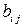 называется антисимметричным, если для любых индексов i и j выполняется равенство:
называется антисимметричным, если для любых индексов i и j выполняется равенство: 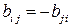 .
.
Произвольный тензор второго ранга 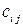 можно представить в виде суммы симметричного и антисимметричного тензоров:
можно представить в виде суммы симметричного и антисимметричного тензоров:
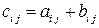
где 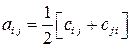 ,
, 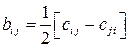
Вектор 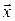 называется собственным вектором симметричной квадратной матрицы
называется собственным вектором симметричной квадратной матрицы 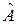 , а
, а 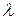 - ее собственным значением, если выполняется условие:
- ее собственным значением, если выполняется условие:
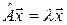
или
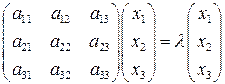
В тензорной алгебре направление, задаваемое вектором 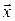 называется главным направлением тензора
называется главным направлением тензора 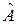 , а
, а 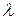 -главным значением тензора.
-главным значением тензора.
Система уравнений, из которой находятся главные направления и главные значения тензора является системой линейных, однородных уравнений относительно компонент вектора 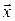 , которая имеет отличное от нуля решение только при условии:
, которая имеет отличное от нуля решение только при условии:
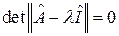
или
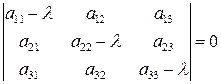
где 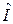 - единичная матрица. Раскрывая определитель, получаем для нахождения главных (собственных) значений тензора алгебраическое уравнение третьей степени (т.е. кубическое уравнение).
- единичная матрица. Раскрывая определитель, получаем для нахождения главных (собственных) значений тензора алгебраическое уравнение третьей степени (т.е. кубическое уравнение).
Можно доказать, что в случае симметричного тензора полученное уравнение всегда имеет три вещественных корня. Возможно, что некоторые из них, совпадают по величине. (В этом случае корни называются кратными или вырожденными.) Если все корни различны, каждому из них однозначно соответствуют направления в пространстве, называемые главными направлениями тензора. В случае вырожденных корней возникает неоднозначность в выборе главных направлений. Так в случае двукратного вырождения корня существует плоскость, проходящая через начало координат, перпендикулярная третьему главному направлению, все направления на которой являются главными. Если вырождение трехкратное, то любые направления в пространстве являются главными. Аналогично, в случае тензоров на плоскости (двумерное пространство) возможны либо два разных вещественных корня, либо эти корни совпадут.
В согласии со сказанным, главные направления (главные оси) симметрического тензора второго ранга всегда можно выбрать взаимно ортогональными. Эти направления выбираются однозначно в случае невырожденных главных значений и неоднозначно в случае вырождения. В системе главных осей тензор диагонален, а на его главной диагонали стоят главные (собственные) значения.
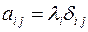
(Следует иметь в виду, что в данном случае суммирование по индексу i не подразумевается).
Для геометрической иллюстрации указанных свойств симметричного тензора второго ранга удобно ввести понятие характеристической поверхности тензора. Ее уравнение имеет вид уравнения, определяющего поверхность второго порядка:
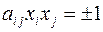
Если все главные значения тензора одинаковы 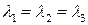 , то такой тензор называется шаровым. Шаровой тензор пропорционален единичному и имеет одинаковый вид во всех системах координат. Характеристическая поверхность шарового тензора есть сфера. Если два главных значения одинаковы, а третье отлично от них
, то такой тензор называется шаровым. Шаровой тензор пропорционален единичному и имеет одинаковый вид во всех системах координат. Характеристическая поверхность шарового тензора есть сфера. Если два главных значения одинаковы, а третье отлично от них 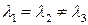 , то тензор называется симметрическим. Его характеристическая поверхность является поверхностью вращения. Если все три собственные значения различны, то такой тензор называется асимметрическим, а его характеристическая поверхность является поверхностью второго порядка общего вида.
, то тензор называется симметрическим. Его характеристическая поверхность является поверхностью вращения. Если все три собственные значения различны, то такой тензор называется асимметрическим, а его характеристическая поверхность является поверхностью второго порядка общего вида.
Если все главные значения тензора положительны, то тензор называется положительно определенным. Если все главные значения отрицательны, то тензор называется отрицательно определенным. В этих случаях при
построении характеристических поверхностей надо выбирать разные знаки в правой части уравнения поверхности (плюс для положительно определенного тензора и минус для отрицательно определенного). И в том, и в другом случаях характеристическая поверхность тензора есть эллипсоид (шар в случае 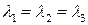 , эллипсоид вращения в случае
, эллипсоид вращения в случае 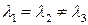 и эллипсоид общего вида в случае
и эллипсоид общего вида в случае 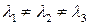 ).
).
Если некоторые собственные значения тензора положительны, а некоторые отрицательны, то тензор называется знаконеопределенным. Его характеристической поверхностью является гиперболоид с двумя листами, отвечающим двум знакам в правой части уравнения для характеристической поверхности.
Для вычисления собственных значений симметричного тензора второго ранга в трехмерном пространстве удобно воспользоваться следующим приемом. Преобразуем уравнение, определяющее собственные значения
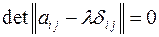
к виду: 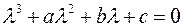
Замена переменной 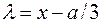 приводит к кубическому уравнению относительно величины
приводит к кубическому уравнению относительно величины 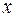 , в котором отсутствует квадратичный член. (Удобно обозначить коэффициенты нового уравнения как –3p и 2q. В случае трех вещественных корней величина p > 0)
, в котором отсутствует квадратичный член. (Удобно обозначить коэффициенты нового уравнения как –3p и 2q. В случае трех вещественных корней величина p > 0)
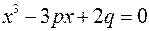
Корни этого уравнения могут быть найдены по формуле:
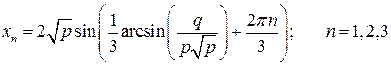
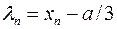
Ее доказательство основано на использовании известного выражения для синуса тройного аргумента: 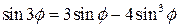 . Запишем данное выражение как тождество:
. Запишем данное выражение как тождество: 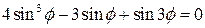 . Сделав в кубическом уравнении замену
. Сделав в кубическом уравнении замену 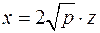 , получим
, получим 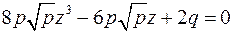 , или
, или
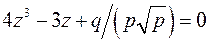 . Сравнение данного уравнения с тригонометрическим тождеством позволяет найти все его корни как
. Сравнение данного уравнения с тригонометрическим тождеством позволяет найти все его корни как 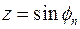 , где
, где 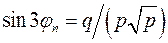 . Отсюда следует, что
. Отсюда следует, что 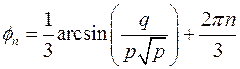
и соответственно: 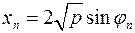 , где n=1,2,3. (Конец доказательства).
, где n=1,2,3. (Конец доказательства).
Собственные векторы симметрического тензора 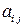 , принадлежащие собственному значению
, принадлежащие собственному значению 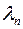 , находим как
, находим как 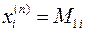 , где
, где 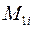 - миноры матрицы
- миноры матрицы 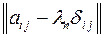 с данным собственным значением
с данным собственным значением 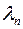 .
.
 2015-04-01
2015-04-01 2743
2743








