4.1 Разложить в двумерном случае тензор второго ранга 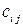 на сумму симметричного
на сумму симметричного 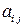 и антисимметричного
и антисимметричного 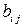 тензоров. Компоненты тензора
тензоров. Компоненты тензора 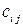 равны:
равны:
4.1.1 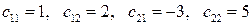
4.1.2 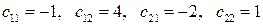
4.1.3 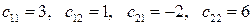
4.1.4 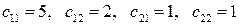
4.1.5 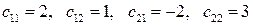
4.1.6 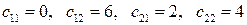
4.2 Разложить тензор второго ранга 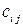 на сумму симметричного
на сумму симметричного 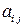 и антисимметричного
и антисимметричного 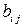 тензоров, где
тензоров, где 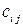 равны
равны
4.2.1 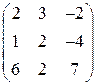 4.2.2
4.2.2 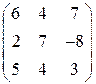
4.2.3 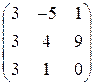 4.2.4
4.2.4 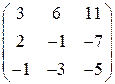
Решение задачи 4.2.1. Используем для данного разложения формулы: 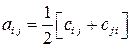 и
и 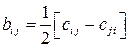 . Непосредственное вычисление компонент симметричного и антисимметричного тензоров дает:
. Непосредственное вычисление компонент симметричного и антисимметричного тензоров дает: 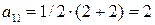 ,
, 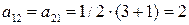 ,
, 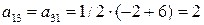 и т.д.
и т.д.
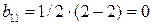 ,
, 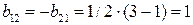 ,
, 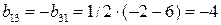 и т.д.
и т.д.
Ответ: 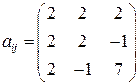 ,
, 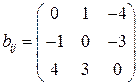
4.3 Для симметричного тензора 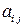 на плоскости:
на плоскости:
4.3.1 Найти собственные значения.
4.3.2 Найти собственные векторы.
4.3.3 Проверить ортогональность собственных векторов.
4.3.4 Найти орты системы координат, связанной с главными осями.
4.3.5 Записать матрицу поворота к главным осям.
4.3.6 Записать вид тензора в главных осях.
4.3.7 Построить характеристическую поверхность.
Произвести вычисления для тензоров с компонентами:
а) 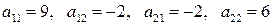
б) 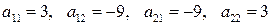
в) 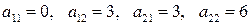
г) 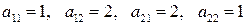
4.4 Разложить тензор 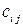 на сумму симметричного
на сумму симметричного 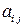 и антисимметричного
и антисимметричного 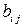 тензоров. Для симметричного тензора
тензоров. Для симметричного тензора 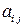 :
:
4.4.1 Найти собственные значения.
4.4.2 Найти собственные векторы.
4.4.3 Проверить ортогональность собственных векторов
4.4.4 Найти орты системы координат, связанной с главными осями.
4.4.5 Записать матрицу поворота к главным осям.
4.4.6 Записать вид тензора в главных осях.
4.4.7 Классифицировать тензор (шаровой, симметрический, асимметрический, положительно, отрицательно определенный или знаконеопределенный).
Произвести вычисления для тензоров 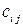 с компонентами:
с компонентами:
a) 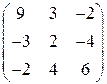 б)
б) 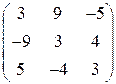
в) 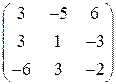 г)
г) 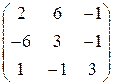
Решение задачи 4.4.1(а) Симметричная часть указанного тензора
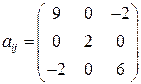 . Составим уравнение
. Составим уравнение 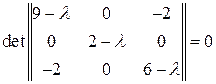
Раскрыв определитель, получим 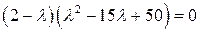 . Нахождение корней этого уравнения
. Нахождение корней этого уравнения 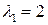 ,
, 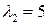 ,
, 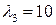 решает поставленную задачу.
решает поставленную задачу.
Решение задачи 4.4.2(а) Проведем вычисление компонент собственного вектора, принадлежащего собственному значению 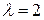 . Для этого следует решить уравнение
. Для этого следует решить уравнение 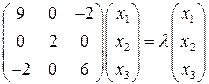 . Подставив
. Подставив 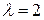 , распишем его как систему трех линейных уравнений
, распишем его как систему трех линейных уравнений 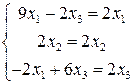 . Отсюда следует, что
. Отсюда следует, что 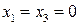 ,
, 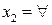 . (Здесь
. (Здесь 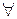 - любое вещественное число, не равное нулю)
- любое вещественное число, не равное нулю)
Аналогично, для 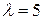 находим
находим 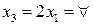 ,
, 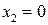 . И, наконец, для
. И, наконец, для 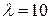 компоненты собственного вектора
компоненты собственного вектора 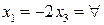 ,
, 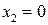 .
.
Решение задачи 4.4.4(а) Используем найденные выше три собственных вектора 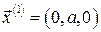 ,
, 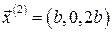 ,
, 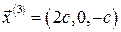 , принадлежащих соответственно собственным значениям 2, 5, 10. Орты системы координат, связанной с главными осями тензора, по определению, это собственные векторы с модулями, равными единице. Очевидно, что при
, принадлежащих соответственно собственным значениям 2, 5, 10. Орты системы координат, связанной с главными осями тензора, по определению, это собственные векторы с модулями, равными единице. Очевидно, что при 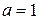 ,
, 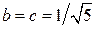 , собственные векторы имеют единичные модули. Поэтому, искомые орты имеют вид:
, собственные векторы имеют единичные модули. Поэтому, искомые орты имеют вид: 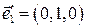 ,
, 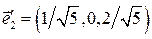 ,
, 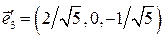
Решение задачи 4.4.5(а) Искомая матрица поворота 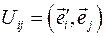 , здесь
, здесь 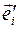 -орты системы главных осей тензора,
-орты системы главных осей тензора, 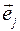 -орты системы координат, в которой заданы компоненты тензора. Учитывая, что
-орты системы координат, в которой заданы компоненты тензора. Учитывая, что 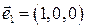 ,
, 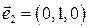 ,
, 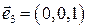 вычислим все возможные скалярные произведения
вычислим все возможные скалярные произведения 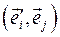 . В итоге мы
. В итоге мы
получим матрицу поворота 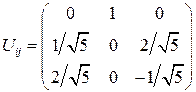 , по строкам которой расположены компоненты орт системы главных осей тензора. Как у любой матрицы поворота ее определитель равен 1. В ряде случаев возможен результат (–1). Тогда, для построения матрицы поворота требуется дополнительно изменить направление одного из орт.
, по строкам которой расположены компоненты орт системы главных осей тензора. Как у любой матрицы поворота ее определитель равен 1. В ряде случаев возможен результат (–1). Тогда, для построения матрицы поворота требуется дополнительно изменить направление одного из орт.
Решение задачи 4.4.6(а) Выполним поворот в систему главных осей тензора. Его компоненты в повернутой системе координат вычисляются как матричное произведение 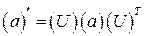 . Воспользуемся матрицей поворота, найденной в ходе решения предыдущей задачи, и вычислим матричное произведение
. Воспользуемся матрицей поворота, найденной в ходе решения предыдущей задачи, и вычислим матричное произведение
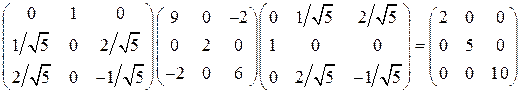
В системе главных осей тензор диагонален, а на его главной диагонали расположены главные (собственные) значения.
4.5 Какая характеристическая поверхность отвечает тензору, у которого
одна (две) главных значения равны 0?
 2015-04-01
2015-04-01 3022
3022








