3.1 Даны скаляр 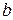 и тензор третьего ранга
и тензор третьего ранга 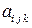 . Доказать,что
. Доказать,что 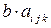 - тензор третьего ранга.
- тензор третьего ранга.
3.2 Даны тензоры второго ранга 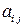 и
и 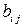 . Доказать, что
. Доказать, что 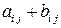 - тензор второго ранга.
- тензор второго ранга.
Решение задачи 3.2 Выполним покомпонентное сложение этих тензоров в повернутой системе координат. 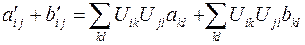 . Или,
. Или, 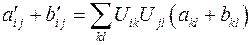 . Отсюда следует, что сумма данных тензоров при повороте системы координат преобразуется по закону преобразования компонент тензора второго ранга, что и требовалось доказать.
. Отсюда следует, что сумма данных тензоров при повороте системы координат преобразуется по закону преобразования компонент тензора второго ранга, что и требовалось доказать.
3.3 Даны векторы 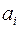 и
и 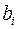 . Доказать, что множество величин
. Доказать, что множество величин 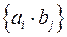 образуют тензор второго ранга. Такой тензор иногда называют диадой.
образуют тензор второго ранга. Такой тензор иногда называют диадой.
Решение задачи 3.3 Составим множество аналогичных величин из компонент векторов 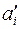 и
и 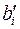 в повернутой системе координат
в повернутой системе координат 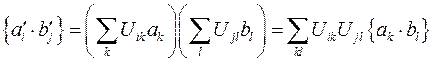 . Отсюда следует, что внешнее произведение двух векторных величин при повороте системы координат преобразуется по закону преобразования компонент тензора второго ранга, что и требовалось доказать.
. Отсюда следует, что внешнее произведение двух векторных величин при повороте системы координат преобразуется по закону преобразования компонент тензора второго ранга, что и требовалось доказать.
3.4 Даны вектор 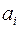 и тензор второго ранга
и тензор второго ранга 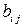 . Доказать, что множество величин
. Доказать, что множество величин 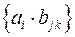 образуют тензор третьего ранга.
образуют тензор третьего ранга.
3.5 Дан вектор 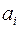 . Показать, что сумма
. Показать, что сумма 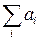 не является скалярной величиной. (Т.е. не имеет тензорную природу).
не является скалярной величиной. (Т.е. не имеет тензорную природу).
Решение задачи 5.5. Рассмотрим конкретный пример, и убедимся, что указанная сумма изменится при повороте системы координат. Пусть в исходной системе координат компонента вектора 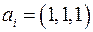 . Модуль данного вектора
. Модуль данного вектора 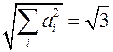 . Повернем систему координат так, чтобы новая ось OX была параллельна данному вектору. Очевидно, что в такой системе координат его компоненты
. Повернем систему координат так, чтобы новая ось OX была параллельна данному вектору. Очевидно, что в такой системе координат его компоненты 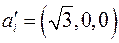 . В исходной системе координат сумма
. В исходной системе координат сумма 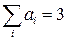 , а в новой, соответственно:
, а в новой, соответственно: 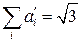 .
.
3.6 Дан тензор второго ранга 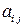 . Доказать, что множество величин, задаваемых равенствами
. Доказать, что множество величин, задаваемых равенствами 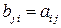 , образует тензор второго ранга.
, образует тензор второго ранга.
3.7 Дан тензор третьего ранга 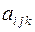 . Доказать, что множество величин
. Доказать, что множество величин 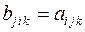 образуют тензор третьего ранга.
образуют тензор третьего ранга.
3.8 Даны скаляр 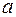 и вектор
и вектор 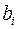 . Доказать, что трехкомпонентная величина
. Доказать, что трехкомпонентная величина 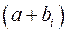 не является величиной тензорной природы.
не является величиной тензорной природы.
3.9 Доказать, что свертка тензора второго ранга 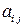 является скаляром:
является скаляром: 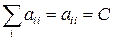 . Такая свертка часто называется следом тензора
. Такая свертка часто называется следом тензора 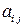 .
.
Замечание. Здесь и в дальнейшем знаки сумм будут зачастую опускаться, и использоваться правило суммирования Эйнштейна.
3.10 Даны тензоры второго ранга 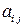 и
и 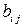 . Доказать, что множество величин
. Доказать, что множество величин 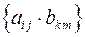 образуют тензор четвертого ранга.
образуют тензор четвертого ранга.
3.11 Найти вектор 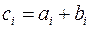 и вектор
и вектор 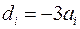 , где векторы
, где векторы 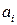 и
и 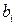 равны:
равны:
3.11.1 
3.11.2 
3.11.3 
3.11.4 
3.12 Найти тензор 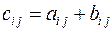 и тензор
и тензор 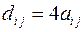 , где
, где 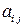 и
и 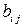 являются тензорами в двумерном пространстве и их компоненты равны:
являются тензорами в двумерном пространстве и их компоненты равны:
3.12.1 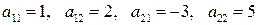
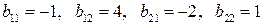
3.12.2 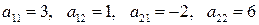
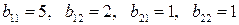
3.12.3 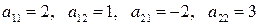
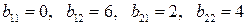
3.13 Вычислить след тензоров 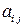 и
и 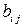 , где тензоры
, где тензоры 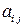 и
и 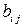 определены в задании 3.12
определены в задании 3.12
3.14 В двумерном пространстве заданы векторы 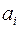 и
и 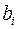 , а так же тензоры второго ранга
, а так же тензоры второго ранга 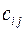 и
и 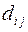 . Найти тензорную размерность приведенных ниже величин и вычислить все их компоненты:
. Найти тензорную размерность приведенных ниже величин и вычислить все их компоненты:
3.14.1 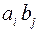 3.14.2
3.14.2 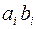
3.14.3 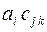 3.14.4
3.14.4 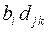
3.14.5 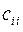 3.14.5
3.14.5 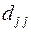
3.17.6 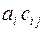 3.14.7
3.14.7 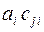
3.14.9 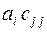 3.14.10
3.14.10 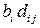
3.14.11 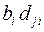 3.14.12
3.14.12 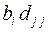
3.14.13 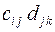 3.14.14
3.14.14 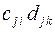
3.14.15 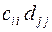 3.14.16
3.14.16 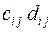
Компоненты векторов 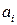 и
и 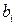 и тензоров
и тензоров 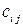 и
и 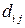 заданы ниже:
заданы ниже:
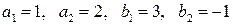
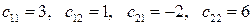
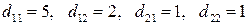
3.15 Тоже, что и в задании 3.14, но для других векторов 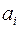 и
и 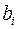 и тензоров
и тензоров 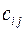 и
и 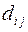 с компонентами:
с компонентами:
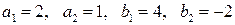
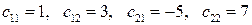
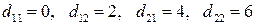
3.16 Тоже, что и в задании 3.14, но для других векторов 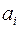 и
и 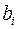 и тензоров
и тензоров 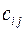 и
и 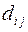 с компонентами:
с компонентами:
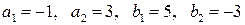
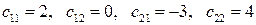
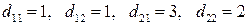
3.17 В случае двумерного пространства убедиться, что след тензора второго ранга (сумма диагональных элементов тензора) в системе координат, повернутой на угол 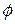 относительно исходной, равен следу тензора в исходной системе координат.
относительно исходной, равен следу тензора в исходной системе координат.
3.18 В случае трехмерного пространства доказать, что след тензора второго ранга одинаков во всех системах координат.
Решение задачи 3.18 Вычислим след тензора в повернутой системе координат.
В данном примере мы не будем опускать символ суммирования по индексам.
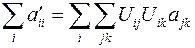 . Используя далее свойство ортогональности матрицы поворота
. Используя далее свойство ортогональности матрицы поворота 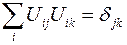 , получим
, получим 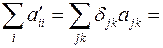
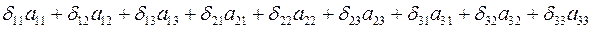 .
.
Так компоненты единичного тензора 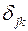 равны единице при совпадающих значениях индексов, и равны нулю в случае несовпадения значений индексов, в данную сумму может внести вклад только первое, пятое и девятое слагаемые. Итого
равны единице при совпадающих значениях индексов, и равны нулю в случае несовпадения значений индексов, в данную сумму может внести вклад только первое, пятое и девятое слагаемые. Итого 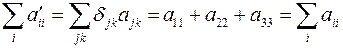 .
.
3.19 Доказать, что множество величин (свертка) 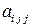 образует вектор, если
образует вектор, если 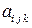 -тензор третьего ранга.
-тензор третьего ранга.
3.20 Доказать, что множество величин (свертка) 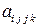 образует тензор второго ранга, если
образует тензор второго ранга, если  -тензор четвертого ранга.
-тензор четвертого ранга.
 2015-04-01
2015-04-01 1542
1542








