Действия над тензорами

Перечислим возможные действия над тензорами, в результате которых возникают также тензорные величины.

1. Если все компоненты некоторого тензора умножить на одинаковую скалярную величину, в результате получится новая многокомпонентная величина, являющаяся тензором того же ранга, что и исходный тензор.

2. Покомпонентное сложение двух тензоров одинакового ранга дает компоненты тензора, называемого суммой исходных тензоров и имеющего тот же ранг. Складывать тензоры различных рангов недопустимо.

3. Если каждая компонента одного тензора ранга N умножается на всевозможные компоненты второго тензора ранга M, возникает многокомпонентная величина, являющаяся тензором ранга N+M. Данная операция называется операцией внешнего произведения тензоров.

4. Если из компонент тензора ранга N 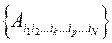выбрать такие компоненты, у которых нумерующие индексы в двух позициях (скажем k и p) одинаковы 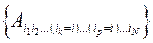, и равны некоторой величине i, после чего сложить выбранные компоненты, отвечающие возможным значениям индекса i, т.е. i=1,2,3, при неизменных нумерующих индексах в других позициях, то полученная многокомпонентная величина:

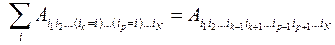
является тензором ранга N-2. Такая операция называется сверткой тензора по индексам, занимающими позиции k и p. Например

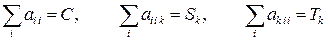
Задание. Показать, что число различных вариантов сверток тензора ранга N равно .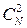

5. Многокомпонентная величина, полученная из исходного тензора ранга N путем перестановки его индексов, является тензором того же ранга. Например, из компонент тензора второго ранга 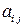можно составить новый тензора второго ранга 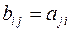. Симметричным называется тензор, компоненты которого не изменяются при перестановке индексов.

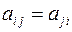
Аналогично, если при перестановке любой пары индексов у любой компоненты тензора возникает компонента, равная исходной по величине и противоположной по знаку, тензор называется антисимметричным.

Задание. Убедиться в том, что в трехмерном пространстве возможны антисимметричные тензоры только 2-го и 3-го рангов.

Для доказательства того, что в результате перечисленных выше действий над тензорами вновь возникают тензоры, необходимо убедиться в том, что компоненты последних преобразуются при преобразовании координат по тензорному закону. Докажем, например, что при свертке тензора 3-го ранга 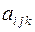возникает тензор ранга (3-2)=1, т.е. вектор. Свернем тензор 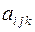, например, по первому и второму индексам. Для этого отберем из 27 компонент 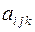те, у которых два первых индекса одинаковы 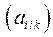и просуммируем по ним при фиксированном значении индекса k. Мы получим три компоненты 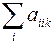. (k=1,2,3). Чтобы доказать, что эти компоненты являются компонентами вектора, необходимо проверить, что они преобразуются по

векторному закону. Выполним свертку тензора 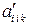в другой системе

координат, которая повернута относительно исходной, и получим:

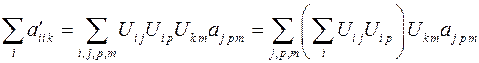
В силу ортогональности матрицы преобразования 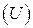имеем:

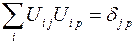
С учетом этого получаем:

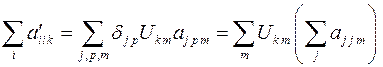
Отсюда следует, что данная свертка при повороте системы координат преобразуется по закону преобразования компонент вектора, что и требовалось доказать.