5.1 Вычислить:
5.1.1 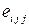 5.1.2
5.1.2 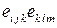
5.1.3 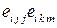 5.1.4
5.1.4 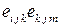
5.1.5 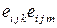 5.1.6
5.1.6 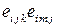
5.1.7 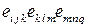 5.1.8
5.1.8 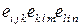
Решение задачи 5.1.5. Используем формулу для свертки: 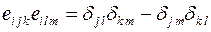 . Положим далее значение индекса
. Положим далее значение индекса 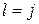 и выполним свертку по паре индексов
и выполним свертку по паре индексов 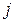 .
. 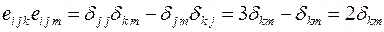 . Здесь использовано, что
. Здесь использовано, что 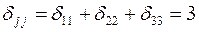 и
и 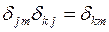 .
.
5.2 Записать формулу для смешанного произведения трех векторов 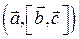 , использую символ Леви-Чивита.
, использую символ Леви-Чивита.
5.3 Получить формулу преобразования двойного векторного произведения 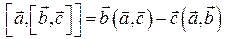 , используя символ Леви-Чивита.
, используя символ Леви-Чивита.
Решение задачи 5.3. Запишем выражение для 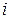 -ой компоненты двойного векторного произведения
-ой компоненты двойного векторного произведения 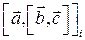 как свертку
как свертку 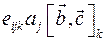 . С учетом, что
. С учетом, что 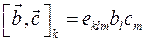 , получим
, получим 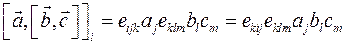 . Далее,
. Далее, 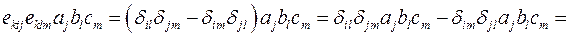
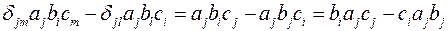 . Или, что
. Или, что
эквивалентно 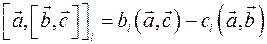 .
.
5.4 Преобразовать выражения, используя символ Леви-Чивита.
5.4.1 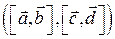 5.4.2
5.4.2 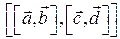
5.4.3 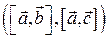 5.4.4
5.4.4 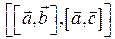
5.4.5 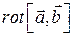 5.4.6
5.4.6 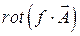
5.4.7 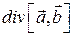 5.4.8
5.4.8 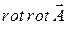
5.4.9 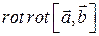 5.4.10
5.4.10 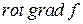
5.4.11 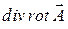
Решение задачи 5.4.6. Воспользуемся выражением для ротора
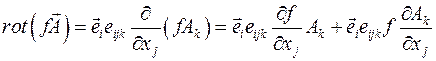 .
.
В силу определения 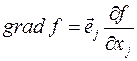 , или
, или 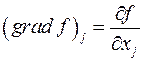 , отсюда следует что
, отсюда следует что 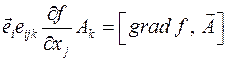 и
и 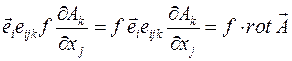 . Итого:
. Итого: 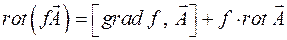
5.5 Вычислить, используя символ Леви-Чивита:
5.5.1 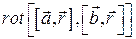 , где
, где 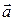 и
и 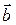 - постоянные векторы.
- постоянные векторы.
5.5.2 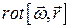 , где
, где 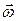 - постоянный вектор.
- постоянный вектор.
5.5.3 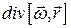 , где
, где 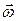 - постоянный вектор.
- постоянный вектор.
5.5.4 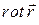
5.5.5 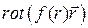
5.5.6 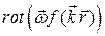 , где
, где 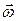 и
и 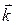 - постоянные векторы.
- постоянные векторы.
5.6 Показать, что определитель матрицы 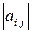 можно записать в виде
можно записать в виде
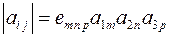 .
.
 2015-04-01
2015-04-01 945
945








