2.1 Найти матрицу преобразования системы декартовых координат 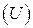 на плоскости при повороте на угол
на плоскости при повороте на угол 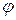 .
.
Решение задачи 2.1 Матричные элементы искомой матрицы вычисляются как скалярные произведения 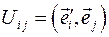 , здесь индексы i,j принимают только два значения: 1 или 2. Так как все орты по определению имеют единичные модули, каждое скалярное произведение равно косинусу угла между соответствующими ортами. Нарисуйте на листе бумаги пояснительный чертеж и убедитесь, что углы между парами базисных орт
, здесь индексы i,j принимают только два значения: 1 или 2. Так как все орты по определению имеют единичные модули, каждое скалярное произведение равно косинусу угла между соответствующими ортами. Нарисуйте на листе бумаги пояснительный чертеж и убедитесь, что углы между парами базисных орт 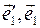 и
и 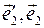 одинаковы и равны углу поворота
одинаковы и равны углу поворота 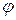 . Поэтому
. Поэтому 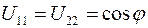 . Угол между ортами
. Угол между ортами 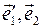 равен
равен 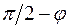 , и соответственно
, и соответственно 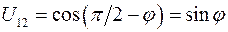 . Угол между ортами
. Угол между ортами 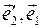 равен
равен 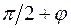 , поэтому
, поэтому 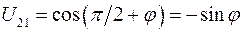 .
.
2.1.1. Убедиться, что определитель матрицы 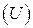 равен 1.
равен 1.
2.1.2 Убедиться, что матрица 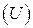 ортогональна, т.е.
ортогональна, т.е. 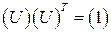 , где
, где 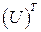 -транспонированная матрица, а
-транспонированная матрица, а 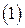 -единичная матрица.
-единичная матрица.
2.1.3 Убедиться, что 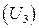 - матрица поворота на угол
- матрица поворота на угол 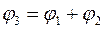 совпадает с произведением матриц
совпадает с произведением матриц 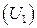 и
и 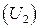 , которые являются матрицами поворота на углы
, которые являются матрицами поворота на углы 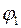 и
и 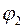 соответственно.
соответственно.
2.1.4. Убедиться, что матрица поворота 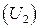 на угол
на угол 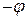 совпадает с матрицей
совпадает с матрицей 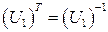 , где
, где 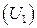 - матрица поворота на угол
- матрица поворота на угол 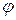 .
.
2.2 Найти матрицу поворота 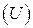 в трехмерном пространстве относительно заданной координатной оси на угол
в трехмерном пространстве относительно заданной координатной оси на угол 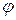 .
.
2.2.1 Вокруг оси Oz
Решение задачи 2.2.1 Очевидно, что базисные орты 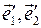 , повернутой вокруг оси Oz системы координат, лежат в Oxy плоскости исходной координатной системы. Выше (см. задачу 2.1) мы уже вычислили скалярные произведения
, повернутой вокруг оси Oz системы координат, лежат в Oxy плоскости исходной координатной системы. Выше (см. задачу 2.1) мы уже вычислили скалярные произведения 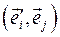 для i,j=1 и 2. Фактически мы нашли соответствующие им матричные элементы искомой матрицы повороты в трехмерном пространстве:
для i,j=1 и 2. Фактически мы нашли соответствующие им матричные элементы искомой матрицы повороты в трехмерном пространстве: 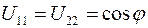 ,
, 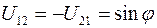 . Для нахождения остальных матричных элементов заметим, что базисные орты
. Для нахождения остальных матричных элементов заметим, что базисные орты 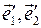 ортогональны орту
ортогональны орту 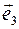 , поэтому
, поэтому 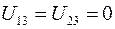 . После выполнения поворота вокруг оси Oz направление аналогичной оси новой системы координат не изменится, т.е. орт
. После выполнения поворота вокруг оси Oz направление аналогичной оси новой системы координат не изменится, т.е. орт 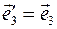 . Оставшиеся матричные элементы вычисляются тривиально:
. Оставшиеся матричные элементы вычисляются тривиально: 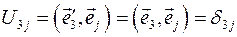 (j=1,2,3). Выпишем явный вид матрицы поворота вокруг оси Oz:
(j=1,2,3). Выпишем явный вид матрицы поворота вокруг оси Oz:
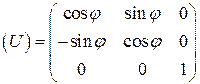
2.2.2 Вокруг оси Ox
Решение задачи 2.2.2 во многом аналогично решению предыдущей задачи.
Приведем в качестве ответа явный вид искомой матрицы поворота:
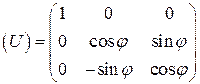
2.2.3 Вокруг оси Oy
2.3 Найти матрицу поворота 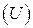 в трехмерном пространстве на углы Эйлера. Углы Эйлера определены следующим образом: вначале проводится поворот на угол
в трехмерном пространстве на углы Эйлера. Углы Эйлера определены следующим образом: вначале проводится поворот на угол 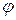 вокруг оси
вокруг оси 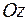 , затем производится поворот на угол
, затем производится поворот на угол 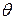 вокруг новой оси
вокруг новой оси 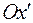 , а после этого производится поворот на угол
, а после этого производится поворот на угол 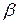 вокруг новой оси
вокруг новой оси 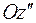 .
.
2.3.1 Доказать, что матрица 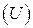 может быть записана в виде произведения трех матриц
может быть записана в виде произведения трех матриц 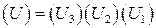 , где матрица
, где матрица 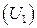 соответствует повороту на угол
соответствует повороту на угол 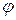 вокруг оси
вокруг оси 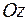 , матрица
, матрица 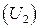 соответствует повороту на угол
соответствует повороту на угол 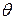 вокруг новой оси
вокруг новой оси 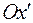 , матрица
, матрица 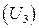 соответствует повороту на угол
соответствует повороту на угол 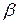 вокруг новой оси
вокруг новой оси 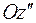 .
.
Решение задачи 2.3.1 Рассмотрим вектор с компонентами 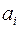 , заданными в исходной системе координат
, заданными в исходной системе координат 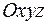 . Объединим его компоненты в матрицу, состоящую из одного столбца
. Объединим его компоненты в матрицу, состоящую из одного столбца 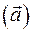 (в так называемый вектор-столбец). Компоненты этого вектора в новой системе координат
(в так называемый вектор-столбец). Компоненты этого вектора в новой системе координат 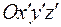 , повернутой вокруг оси
, повернутой вокруг оси 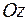 на угол
на угол 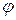 , вычислим как матричное произведение
, вычислим как матричное произведение 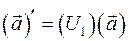 . Давайте рассматривать повернутую систему координат как новую исходную, и совершим далее поворот вокруг ее оси
. Давайте рассматривать повернутую систему координат как новую исходную, и совершим далее поворот вокруг ее оси 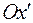 на угол
на угол 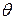 . Компоненты вектора в новой, повернутой системе координат
. Компоненты вектора в новой, повернутой системе координат 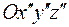 вычислим как матричное произведение
вычислим как матричное произведение 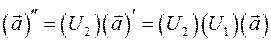 .
.
Матрица поворота 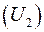 составлена из косинусов углов между ортами новой исходной, и новой повернутой координатных систем. Для ее вычисления мы фактически должны повторить решение задачи 2.2.2 и получить в результате ту же матрицу с заменой угла
составлена из косинусов углов между ортами новой исходной, и новой повернутой координатных систем. Для ее вычисления мы фактически должны повторить решение задачи 2.2.2 и получить в результате ту же матрицу с заменой угла 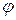 на
на 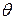 . Давайте примем систему координат
. Давайте примем систему координат
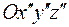 за новую исходную, и выполним последний поворот вокруг оси
за новую исходную, и выполним последний поворот вокруг оси 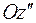 на угол
на угол 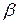 . Компоненты вектора в системе координат
. Компоненты вектора в системе координат 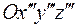 теперь вычисляются как
теперь вычисляются как 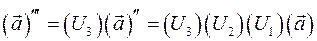 .
.
Матрица 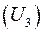 составлена их косинусов углов между соответствующими ортами. Она совпадает с матрицей поворота вокруг оси Oz, найденной в ходе решения задачи 2.2.1, с заменой угла
составлена их косинусов углов между соответствующими ортами. Она совпадает с матрицей поворота вокруг оси Oz, найденной в ходе решения задачи 2.2.1, с заменой угла 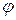 на
на 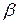 . Итого:
. Итого: 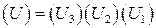 . Приведем для справки явный вид матрицы поворота на углы Эйлера
. Приведем для справки явный вид матрицы поворота на углы Эйлера 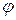 ,
, 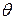 ,
, 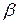 .
.
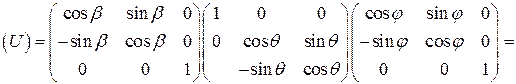
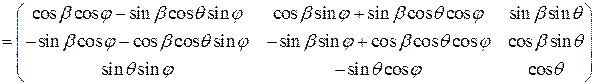
2.3.2 Доказать, что 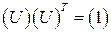 .
.
2.3.3 Выразить матрицу обратного преобразования через произведение матриц поворотов вокруг осей Ox и Oz.
2.4 Найти матрицу 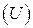 для следующих углов Эйлера:
для следующих углов Эйлера:
2.4.1 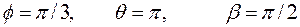
2.4.2 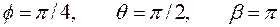
2.4.3 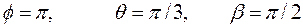
2.4.4 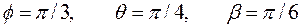
2.4.5 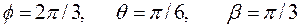
2.4.6 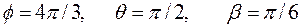
2.5 В случае двумерного пространства вычислить компоненты вектора 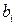 в системе координат повернутой на угол
в системе координат повернутой на угол 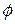 по сравнению с исходной. Компоненты вектора и угол
по сравнению с исходной. Компоненты вектора и угол 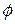 следующие:
следующие:
2.5.1 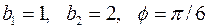
2.5.2 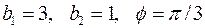
2.5.3 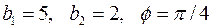
2.5.4 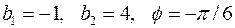
2.5.5 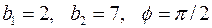
2.5.6 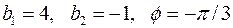
2.6 В случае двумерного пространства вычислить компоненты тензора второго ранга 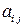 в системе координат, повернутой на угол
в системе координат, повернутой на угол 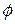 по сравнению с исходной. Компоненты тензора и угол
по сравнению с исходной. Компоненты тензора и угол 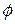 следующие:
следующие:
2.6.1 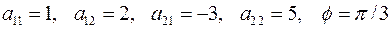
2.6.2 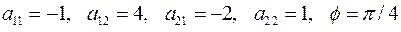
2.6.3 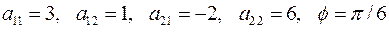
2.6.4 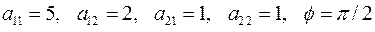
2.6.5 
2.6.6 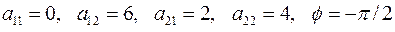
2.7 В трехмерном пространстве заданы компоненты вектора. Найти
компоненты вектора в системе координат, повернутой на угол 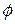 вокруг оси Ox
вокруг оси Ox
по сравнению с исходной. Компоненты вектора и угол 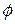 следующие:
следующие:
2.7.1 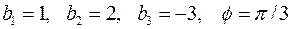
2.7.2 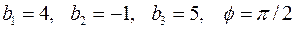
Решение задачи 2.7 дается общей формулой:
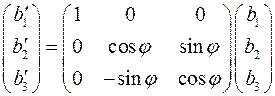
Для конкретного варианта, указанного в пункте 2.7.1 получаем
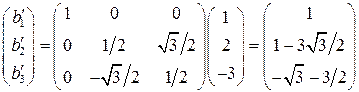
2.8 В трехмерном пространстве заданы компоненты вектора. Найти компоненты вектора в системе координат, повернутой на угол 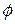 вокруг оси Oy по сравнению с исходной. Компоненты вектора и угол
вокруг оси Oy по сравнению с исходной. Компоненты вектора и угол 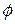 следующие:
следующие:
2.8.1 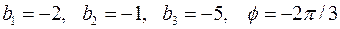
2.8.2 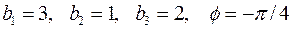
2.9 В трехмерном пространстве заданы компоненты вектора. Найти компоненты вектора в системе координат, повернутой на угол 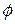 вокруг оси Oz по сравнению с исходной. Компоненты вектора и угол
вокруг оси Oz по сравнению с исходной. Компоненты вектора и угол 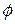 следующие:
следующие:
2.9.1 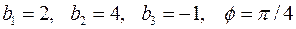
2.9.2 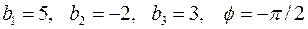
2.10 В случае двумерного пространства найти компоненты тензора 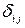 в системе координат, повернутой относительно исходной на угол
в системе координат, повернутой относительно исходной на угол 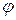 .
.
 2015-04-01
2015-04-01 1753
1753
