Преобразование тензорных величин при инверсии

До сих пор мы рассматривали преобразование тензоров только при повороте системы координат. В этом случае выведенная в разделе 2 матрица преобразования 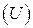ортогональна. Из условия ортогональности 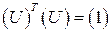следует, квадрат определителя матрицы 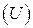равен 1, а сам определитель 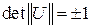. Поворот системы координат на конечный угол можно рассматривать как суперпозицию ряда поворотов на малые углы. Поскольку матрица поворота на малый угол близка к единичной матрице, ее определитель равен 1. Матрица поворота на конечный угол строится как произведение матриц поворотов на малые углы, поэтому ее определитель тоже равен 1, т.е. при любых поворотах на конечный угол .

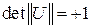Ортогональные преобразования, для которых выполняется последнее равенство, называются собственными. Если определитель равен -1, то такие преобразования называются несобственными. Несобственные преобразования возникают при последовательном проведении поворота и инверсии системы координат. При инверсии направления всех ортов изменяются на противоположные:

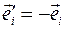
так что матрица преобразования системы координат в случае инверсии равна:

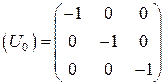
Отсюда ясно, что 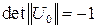, Таким образом, любое ортогональное преобразование, матрица которого равна 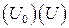, где 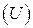- матрица поворота, имеет определитель равный –1.

Закон преобразования компонент истинных тензоров при любых ортогональных преобразованиях координат (как собственных, так и несобственных) имеет вид:

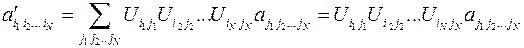
При решении ряда физических задач, помимо истинных тензоров необходимо вводить в рассмотрение псевдотензоры, т.е. многокомпонентные величины, закон преобразования которых имеет вид:

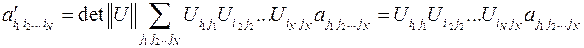
Этот закон преобразования не отличается от закона преобразования тензора в случае собственных ортогональных преобразований при 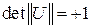, но в случае несобственных преобразований истинные тензоры и псевдотензоры преобразуются по разному закону.

Псевдотензор первого ранга называется псевдовектором. Псевдовекторы нередко называют аксиальными векторами, а истинные векторы полярными. Если представить вектор, как направленный отрезок, то псевдовектор следует считать отрезком параллельным заданной линии, но не имеющим определенного направления. Направление отрезка,

соответствующего псевдовектору, обычно доопределяют с учетом той координатной тройки, которая используется при работе. Псевдовектором является векторное произведение двух истинных векторов, определенное по правилу правой руки, если используется правая система координат, так как направление отрезка в этом случае определяется выбором именно правой тройки ортов координатной системы.

Псевдовекторами являются, например, момент импульса и момент силы, магнитный дипольный момент, напряженность магнитного поля. Истинными векторами являются радиус-вектор, сила, скорость, ускорение, напряженность электрического поля.

Символ Леви-Чивита, является псевдотензором третьего ранга. Для проверки этого утверждения найдем компоненты символа Леви-Чивита 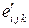в иной декартовой системе координат, считая, что этот символ преобразуется по закону преобразования псевдотензора третьего ранга:

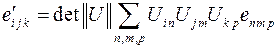
Рассмотрим это равенство для случая, если i=1, j=2, k=3. Согласно задаче 5.6 сумма, фигурирующая в правой части последнего равенства, является определителем матрицы 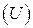. Отсюда ясно, что 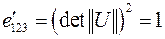. Антисимметричность символа Леви-Чивита 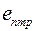относительно перестановки любой пары индексов n,m,p автоматически влечет антисимметричность величин 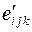, определенных законом преобразования псевдотензора третьего ранга. Поэтому, величины 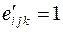, для i,j,k=123,231,312 и 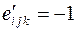для i,j,k=213,132, 321 и равны нулю в случае, если значения индексов совпадают. Таким образом, компоненты символа Леви-Чивита не зависят от выбора

системы координат, что согласуется с их определением, если они преобразуются как псевдотензор третьего ранга.

Действия над тензорами, описанные в разделе 3, обобщаются на случай псевдотензоров:

1. Покомпонентное сложение возможно в случае, когда оба слагаемых являются тензорами или псевдотензорами одинакового ранга. Покомпонентное сложение тензоров и псевдотензоров одинакового ранга в физических уравнениях принципиально возможно. Но “закон природы”, описанный такими уравнениями, не симметричен относительно зеркальных отражений.

2. Внешнее произведение тензора и псевдотензора дает псевдотензор суммарного ранга. Внешнее произведение двух псевдотензоров дает тензор суммарного ранга.

3. Операция свертки псевдотензора по паре одинаковых индексов дает псевдотензор ранга, на два меньше исходного.

4. При перестановке индексов в псевдотензоре получается псевдотензор того же ранга.