2015-04-01
581
6.1 Найти матрицу преобразования, включающую вначале поворот на 900 вокруг оси Oz, а затем инверсию.
Решение задачи 6.1 Искомая матрица преобразования строится как произведение двух матриц: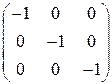 
и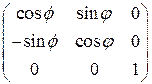 
.
Правая матрица определяет преобразование системы координат при повороте вокруг оси OZ на угол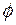 
. (См решение задачи 2.2.3). Левая матрица –
определяет преобразование системы координат при инверсии. Найдем их произведение для конкретного значения угла поворота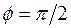 
,
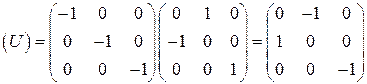
6.2 Как преобразуются компоненты псевдовектора при инверсии?
Решение задачи 6.2 При инверсии системы координат компоненты псевдовектора преобразуются по закону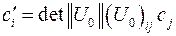 
, где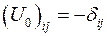 
. Учитывая, что определитель матрицы 
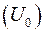равен –1, получим
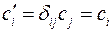. При инверсии системы координат компоненты псевдовекторов не изменяются (в отличие от векторов, компоненты которых изменят знак).
6.3 Даны: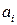 
истинный вектор и 
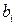- псевдовектор. Чем является их векторное произведение - вектором или псевдовектором?
6.4 Даны: 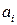, 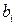и 
- и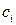стинные векторы. Что представляет собой их смешанное произведение 
?
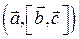6.5 Даны: 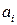и - и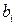стинные векторы, 
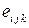- псевдотензор Леви-Чивита. Что представляет собой многокомпонентная величина 
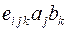? Почему? Какие операции производятся при получении этой величины?
Решение задачи 6.5 В результате выполнения свертки по двум парам индексов j,k внешнего произведения псевдотензора 3-го ранга 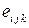и тензора 2-го ранга 
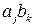должен получиться псевдотензор 1-го ранга (псевдовектор). Убедимся в этом. Выполним такую свертку в иной декартовой координационной системе 
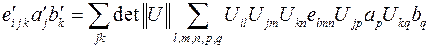. Мы воспользовались
законами преобразования компонент символа Леви-Чивита и векторов. Учтем ортогональность матрицы преобразования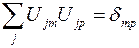 
, 
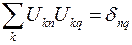, и просуммируем по индексам j,k. В результате получим:
.
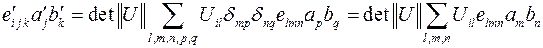Данное выражение можно записать более компактно как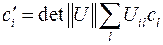 
, где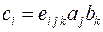 
. Что и подтверждает законность операций внешнего произведения и свертки, в результате которых получается псевдотензор 1-го ранга .
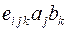6.6 Даны: 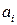- псевдовектор, 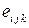- псевдотензор Леви-Чивита. Что представляет собой многокомпонентная величина 
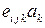? Почему?
6.7 Даны: 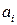- истинный вектор, 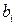- псевдовектор. Что представляет собой величина 
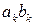? Почему?
7. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА.
Закон преобразования компонент радиус-вектора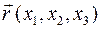 
при ортогональном преобразовании декартовой системы координат имеет тот же вид, что и закон преобразования любого вектора (см. раздел 2):
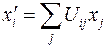
Рассмотрим новые координаты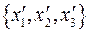 
как функции координат
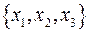(т.е.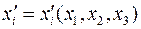 
), мы видим, что:
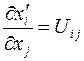
Матрица обратного преобразования определяется матричными элементами:
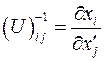
Поскольку матрица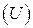 
ортогональна, то
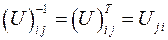
таким образом, в случае ортогональных преобразований:
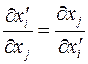
Теперь можно строго доказать, что частные производные скалярного поля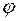 
в каждой точке пространства являются компонентами векторного поля 
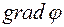. Компоненты градиента в новой системе координат 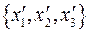равны: 
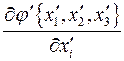. При этом 
.
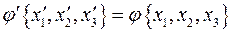Переходя от новых координат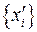 
, к исходным координатам 
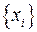получаем:
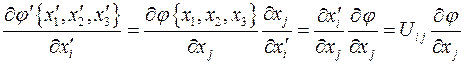
Итак, мы видим, что величины: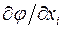 
в самом деле, преобразуются по закону преобразования векторных величин.
Аналогично доказывается, что многокомпонентные величины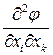 
и 
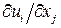, где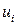 
- компоненты векторного поля, являются тензорами второго
ранга. Тензор второго ранга 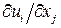в общем случае не является ни симметричным, ни антисимметричным тензором. Его, однако, можно представить в виде суммы симметричного и антисимметричного тензоров:
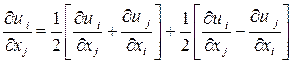
Антисимметричный тензор второго ранга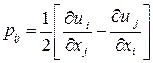 
имеет три отличные от нуля компоненты. Вследствие этого бывает удобно вместо тензора 
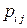ввести псевдовектор, определенный равенством: 
.
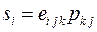Симметричный тензор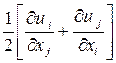 
удобно представить в виде суммы шарового тензора и симметричного тензора, имеющего нулевой след (тензора девиации 
):
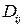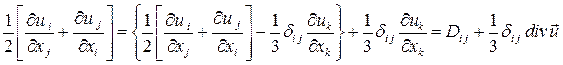
Для тензорного поля 
N-го ранга справедлива обобщенная теорема Остроградского-Гаусса.
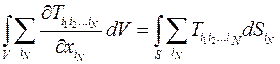(7.1)
