2015-04-01
4221
Задача 3.2.1 Определить напряжение на сопротивлении R интегрирующей RL -цепи (см.рисунок 3.2), если напряжение на входе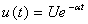 
В(см. рисунок 3.3), параметры:U=50В, α=50с-1, R=47Oм, L=0,25Гн
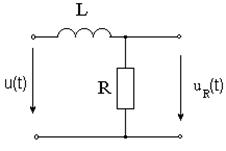
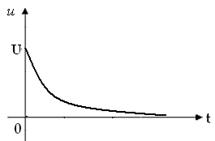
Рисунок 3.2 Рисунок 3.3
Решение: Выбираем аналитическое выражение интеграла Дюамеля (3.3)
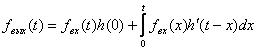(3.10)
Конкретизируя величины, входящие в интеграл Дюамеля, получаем
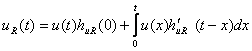(3.11)
Определяем переходную характеристику по напряжению на сопротивлении R
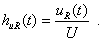(3.12)
Используем известное выражение переходного тока для цепи RL, при подключении ее к источнику постоянного напряжения
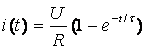(3.13)
Тогда напряжение на сопротивлении в переходном режиме
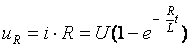(3.14)
где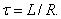 
Следовательно,
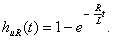(3.15)
Вычисляем компоненты, входящие в интеграл Дюамеля:
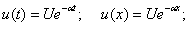
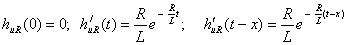
Производя интегрирование в соответствии с выражением (3.11), находят искомое напряжение
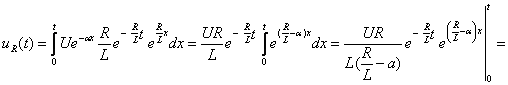
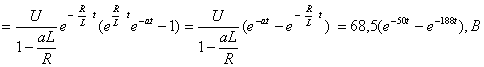(3.16)
Графическое изображение выходного напряжения, построенное в среде Mathcad, показано на рисунке. 3.4.
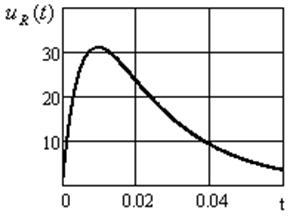
Рисунок 3.4
Задача 3.2.2 На вход цепи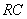 
(см.рисунок 3.5) подается прямоугольный видеоимпульс 
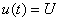(см. рисунок 3.6) с параметрами U= 10В, 
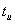=2мс. Параметры RC -цепи: R= 100 Ом; С= 2 5мкФ. Найти уравнения напряжения на конденсаторе и тока в цепи, построить графики.
|
|
|
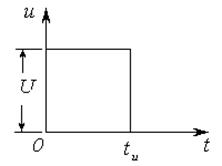
Рисунок 3.5 Рисунок 3.6
Решение: Используем известное выражение переходного напряжения для цепи RС, при подключении ее к источнику постоянного напряжения
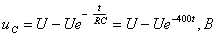, (3.17)
Определяем переходную характеристику по напряжению на емкости
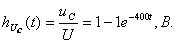(3.18)
Запишем выражения для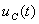 
с помощью интеграла Дюамеля в интервале времени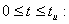 
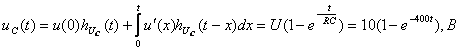(3.19)
так как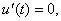 
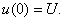
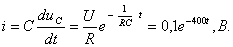(3.20)
В интервале времени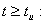 
(3.21)
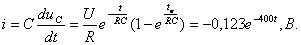(3.22)
Графики для интервала времени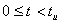 
строим по формулам (3.19), (3.20). Для интервала времени 
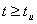графики строят по формулам (3.21) и (3.22).
Графическое изображение выходного напряжения и тока, построенное в среде Mathcad, показано на рисунках. 3.7, 3.8.
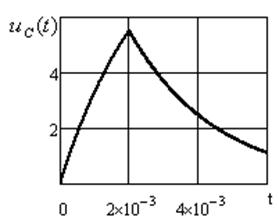
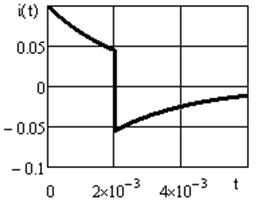
Рисунок 3.7 Рисунок 3.8
Задача 3.2.3 На вход цепи 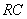(см. рисунок 3.9) с параметрами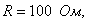 
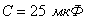подается напряжение, изменяющееся по закону 
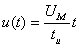(см. рисунок 3.10), где 
, 
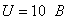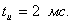Найти уравнения напряжения на конденсаторе и тока в цепи, построить графики.
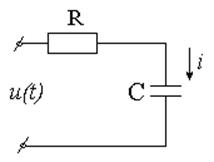
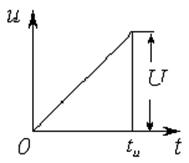
Рисунок 3.9 Рисунок 3.10
Решение: В расчетах используем, найденную в предыдущей задаче, переходную характеристику по напряжению на емкости
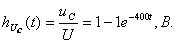(3.23)
Рассмотрим интервал времени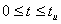 
:
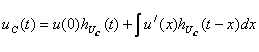(3.24)
где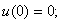 
; 
.
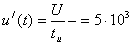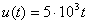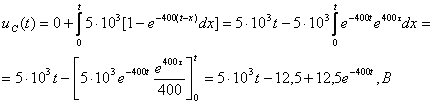(3.25)
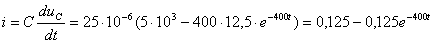, А (3.26)
Рассмотрим интервал времени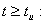
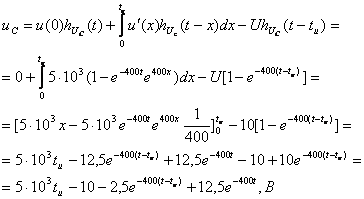(3.27)
Подставив в последнее выражение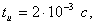 
получим
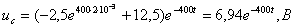(3.28)
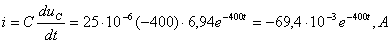(3.29)
Графики для интервала времени 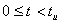строим по формулам (3.25), (3.26); для интервала времени 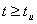по формулам (3.28), (3.29). Построение произведено в среде Mathcad (см. рисунки 3.11, 3.12).
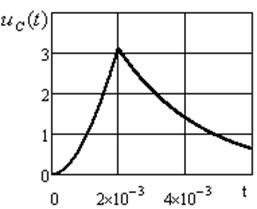
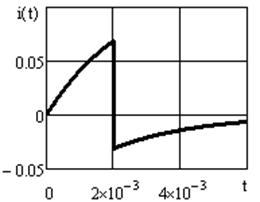
Рисунок 3.11 Рисунок 3.12
Задача 3.2.4 Электрическая цепь (см.рисунок 3.13), параметры которой равны: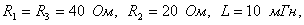 
подключается на импульс напряжения с 
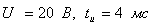(см. рисунок 3.14). Найти выражение тока 
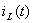на индуктивности.
|
|
|
Решение: 1. Определение переходной характеристики для тока в ветви с индуктивностью.
Для определения переходной проводимости цепи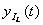 
рассчитаем переходной процесс при подключении цепи при нулевых начальных условиях 
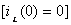к источнику единичного постоянного напряжения (см. рисунок 3.15) и определим ток .
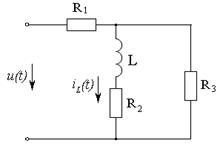
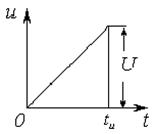
Рисунок 3.13 Рисунок 3.14
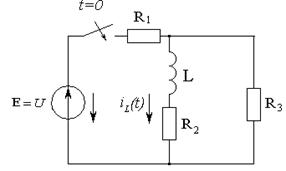
Рисунок 3.15
Независимое начальное условие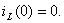 
Ток в переходном режиме в индуктивности можно записать в виде
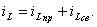(3.30)
Принужденная составляющая тока
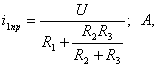
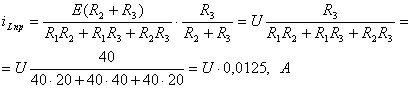(3.31)
Для определения свободной составляющей тока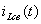 
составим характеристическое уравнение цепи после коммутации методом входного сопротивления относительно ветви с индуктивностью (см. рисунок 3.16).
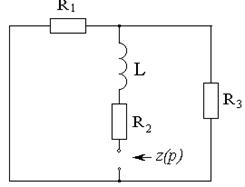
Рисунок 3.16
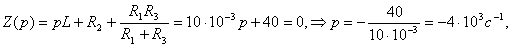(3.32)
тогда,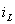 
(t):
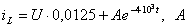(3.33)
Для определения постоянной интегрирования, перепишем выражение (3.33) для момента времени t=0, откуда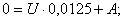 
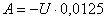, значит
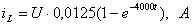(3.34)
Определяем переходную характеристику для тока в ветви с индуктивностью
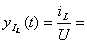
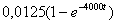(3.35)
2. Определение тока 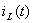при включения цепи на импульс напряжения 
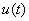с помощью интеграла Дюамеля.
Напряжения 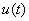имеет разные аналитические выражения в разных интервалах времени
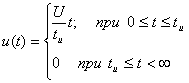
Рассмотрим интервал времени 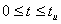(не включая скачок напряжения): 
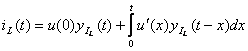(3.36)
где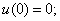 
; 
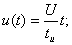
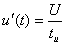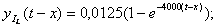
(3.37)
Рассмотрим интервал времени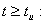
(3.38)
(3.39)
График для интервала времени 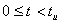строим по формуле (3.37); для интервала времени 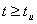по формуле (3.39). Построение произведено в среде Mathcad (см. рисунок 3.17).
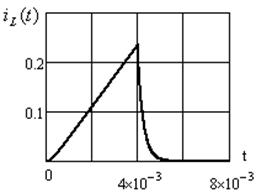
Рисунок 3.17
