2015-04-01
1467
4.1.1 Преобразования Фурье.При воздействии на цепь сигналов произвольной формы широко используется спектральный (частотный) метод анализа электрических цепей. Спектральный метод позволяет определять спектр входного воздействия и вычислять спектральную плотность реакции цепи по спектру входного воздействия и соответствующей комплексной функции передачи цепи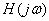 
, а также находить реакцию цепи в переходном и установившемся режимах.
Математической основой спектрального метода анализа электрических цепей являются преобразования Фурье. Непериодическая функция, удовлетворяющая условию абсолютной интегрируемости в бесконечных пределах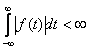 
, может быть представлена интегралом Фурье:
(4.1)
Внутренний интеграл в выражении (4.1) является спектром или спектральной плотностью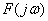 
заданной функции 
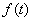и называется прямым преобразованием Фурье:
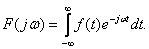(4.2)
Заданную функцию 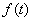можно определить по спектру 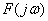с помощью обратного преобразования Фурье:
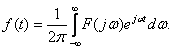(4.3)
Одностороннее обратное преобразование Фурье (если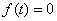 
при 
):
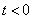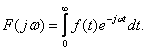(4.4)
Спектральная плотность 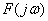является комплексной функцией частоты и может быть записана в показательной форме: 
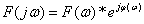, где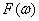 
− амплитудно-частотная характеристика АЧХ (чётная функция частоты),
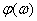− фазочастотная характеристика ФЧХ (нечётная функция частоты).
Обратное преобразование Фурье в тригонометрической форме:
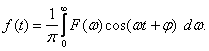(4.5)
Сравнивая прямое и обратное преобразование Лапласа с прямым (4.3) и обратным преобразованием Фурье (4.4), можно сделать вывод, что преобразования Фурье являются частным случаем преобразований Лапласа и получаются из него при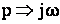 
.
4.1.2 Некоторые свойства преобразований.
Фурье теорема линейности: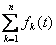 
;
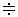
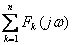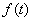
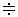
спектры производной и интеграла: если 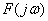, то 
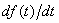
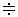
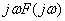и
;
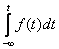
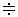
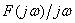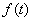
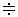
теорема запаздывания: если 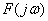, то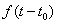 
.
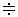
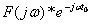4.1.3 Определение спектра непериодических функций.Спектры непериодических входных воздействий определяют по формуле прямого преобразования Фурье или используя таблицы операторных изображений по Лапласу, в которых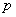 
заменяют на 
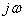. Пример в задаче 4.1.
4.1.4 Определение спектральной плотности реакции цепи.Спектральную плотность реакции цепи вычисляют по спектральной плотности входного воздействия и соответствующей комплексной функции передачи цепи.
Расчет спектра тока в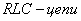 
, закон Ома для частотных спектров при нулевых начальных значениях):
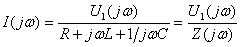(4.6)
где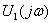 
- спектр непериодического входного воздействия;
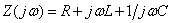- комплексное сопротивление , которое применялось ранее для расчёта установившихся гармонических процессов.
Расчет спектра тока двухполюсника:
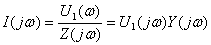(4.7)
где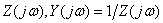 
- комплексные входные сопротивление и проводимость.
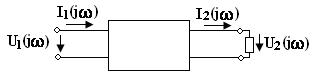
В общем случае спектральную плотность реакции цепи (напряжение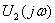 
или ток 
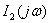произвольного элемента цепи) вычисляют по спектральной плотности входного воздействия по формулам 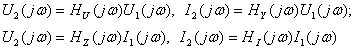(4.8):
(4.8)
где ,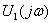 
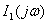- спектры непериодических входных воздействий (напряжения и тока);
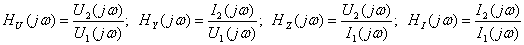- комплексные передаточные функции цепи.
Для расчёта комплексных передаточных функций цепи применяется комплексный метод, который применялся ранее для расчёта установившихся гармонических процессов Примеры в задачах 4.2; 4.
4.1.5 Определение реакции цепи в переходном и установившемся режимах. Спектральный метод может быть применён для расчета переходных процессов в линейных электрических цепях, так как преобразования Фурье являются частным случаем преобразований Лапласа и получаются из него при .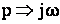
Порядок расчета переходных процессов спектральным методом:
а) определение спектра входного воздействия;
б) определение соответствующей передаточной функции цепи;
в) определение спектра реакции цепи;
г) определение реакции цепи по её спектру с помощью обратного преобразования Фурье, по таблице, по теореме разложения.
Примеры в задачах 4.2; 4.
