Задача 4.1 Определить спектральную плотность 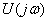 , АЧХ
, АЧХ 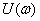 , ФЧХ
, ФЧХ 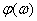 прямоугольного видеоимпульса с амплитудой U и длительностьюtu (см. рисунок 4.1, а, б, в).
прямоугольного видеоимпульса с амплитудой U и длительностьюtu (см. рисунок 4.1, а, б, в).
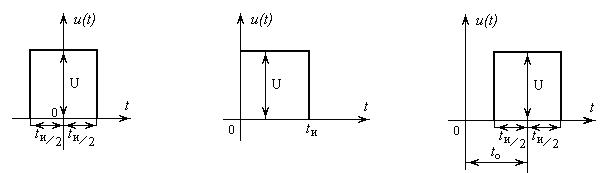
а) б) в)
Рисунок 4.1
Решение: Спектр 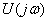 определяют, используя прямое преобразование Фурье
определяют, используя прямое преобразование Фурье
а) для видеоимпульса (см. рисунок 4.1,а):
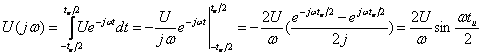 , (4.9)
, (4.9)
АЧХ: 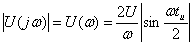 ; ФЧХ:
; ФЧХ: 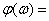 0,если
0,если 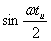 и
и 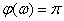 , если
, если 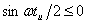 .
.
б) для видеоимпульса (см. рисунок 4.1,б), применяя теорему запаздывания, получают:
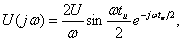 АЧХ:
АЧХ: 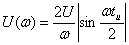 , ФЧХ
, ФЧХ 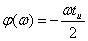 , если
, если 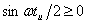 и
и 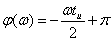 , если
, если 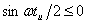 .
.
в) для видеоимпульса (см. рисунок 4.1,в), применяя теорему запаздывания, получают:
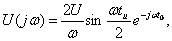 АЧХ:
АЧХ: 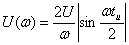 ; ФЧХ:
; ФЧХ: 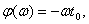 если
если 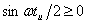 и
и 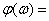
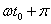 , если
, если 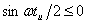 .
.
Графики АЧХ (см. рисунок 4.2) для видеоимпульсов (см. рисунок 4.1, а, б, в), ФЧХ (см. рисунки 4.3; 4.4) для видеоимпульсов (см. рисунок 4.1, а, б) с амплитудой U=20B и длительностью импульса tu=0,004c построены в среде Mathcad.
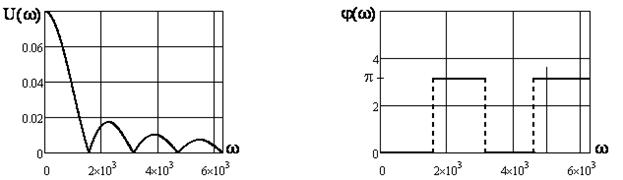
Рисунок 4.2 Рисунок 4.3
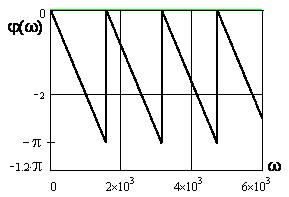
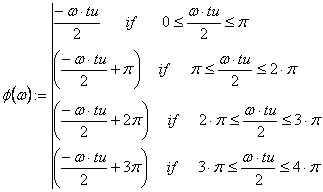
Рисунок 4.4
Задача 4.2 На входе электрической цепи (см. рисунок 4.5), параметры которой 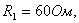
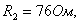
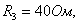
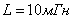 , действует прямоугольный импульс
, действует прямоугольный импульс 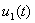 амплитудой
амплитудой 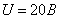 и длительностью
и длительностью 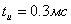 (см. рисунок 4.6).
(см. рисунок 4.6).
Определить комплексную передаточную функцию по напряжению 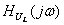 и спектральную плотность напряжения
и спектральную плотность напряжения 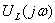 .
.
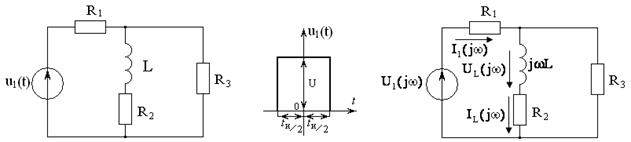
Рисунок 4.5 Рисунок 4.6 Рисунок 4.7
Решение: 1) Определение спектральной плотности входного напряжения.
Спектр входного напряжения найден в задаче 4.1: 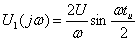 ,
,
АЧХ: 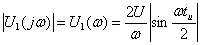 ; ФЧХ:
; ФЧХ: 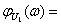 0,если
0,если 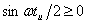 и
и 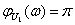 , если
, если 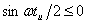 .
.
2) Определение комплексной передаточной функции по напряжению 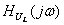 Комплексную передаточную функцию находят по формуле:
Комплексную передаточную функцию находят по формуле: 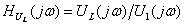 . Будем считать, что на вход цепи подано синусоидальное напряжение, комплексное действующее значение которого
. Будем считать, что на вход цепи подано синусоидальное напряжение, комплексное действующее значение которого 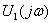 . Применяя комплексный метод расчёта, определяют комплексное действующее значение напряжение
. Применяя комплексный метод расчёта, определяют комплексное действующее значение напряжение 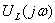 (см. рисунок 4.7) и
(см. рисунок 4.7) и 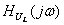 :
:
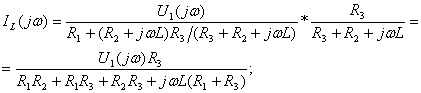
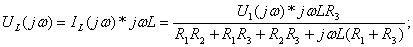 (4.10)
(4.10)
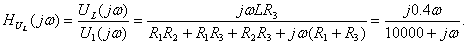 (4.11)
(4.11)
АЧХ: 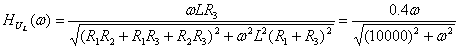
ФЧХ: 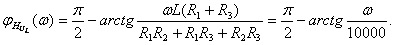
3) Определение спектральной плотности 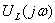 по спектру входного напряжения
по спектру входного напряжения 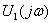 и соответствующей комплексной функции передачи
и соответствующей комплексной функции передачи 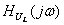 . Спектральную плотность
. Спектральную плотность 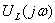 находят по формуле:
находят по формуле:
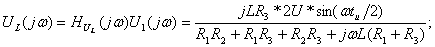 (4.12)
(4.12)
АЧХ: 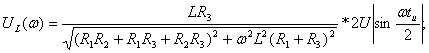
ФЧХ: 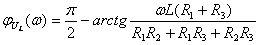 , если
, если 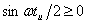 и
и
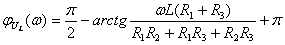 , если
, если 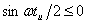 .
.
Подставляют числовые значения: 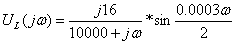 ,
, 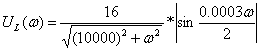 ,
, 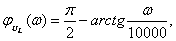 если
если 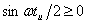 и
и 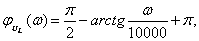 если
если 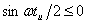 .
.
4) Графики АЧХ: 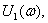
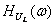 ,
, 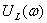 (см. рисунки 4.8, 4.10, 4.12) и ФЧХ
(см. рисунки 4.8, 4.10, 4.12) и ФЧХ 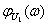 ,
, 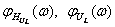 (см. рисунки 4.9, 4.11, 4.13) построены в среде Mathcad.
(см. рисунки 4.9, 4.11, 4.13) построены в среде Mathcad.
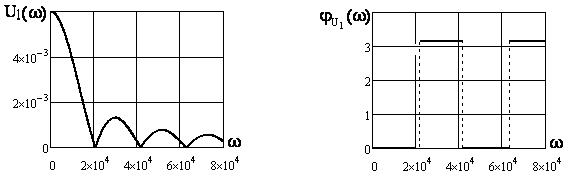
Рисунок 4.8 Рисунок 4.9
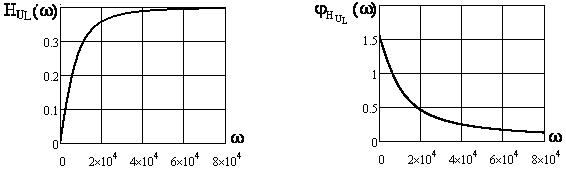
Рисунок 4.10 Рисунок 4.11
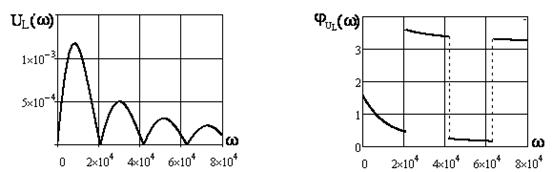
Рисунок 4.12 Рисунок 4.13
Задача 4.3 На входе электрической цепи (см. рисунок 4.15), параметры которой 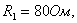
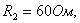
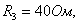
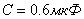 , действует импульс напряжения
, действует импульс напряжения 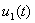 (см. рисунок 4.14) c
(см. рисунок 4.14) c 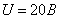 и α=900 c-1.
и α=900 c-1.
Определить:
1) спектральную плотность импульса напряжения 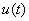 , АЧХ,ФЧХ;
, АЧХ,ФЧХ;
2) комплексную передаточную функцию по напряжению 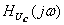 , АЧХ,ФЧХ;
, АЧХ,ФЧХ;
3) спектральную плотность реакции цепи 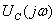 ,АЧХ,ФЧХ;
,АЧХ,ФЧХ;
4) реакцию цепи 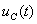 .
.
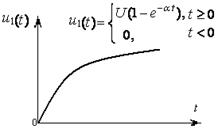
Рисунок 4.14
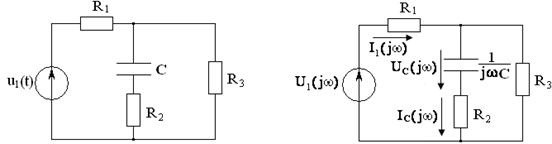
Рисунок 4.15 Рисунок 4.16
Решение: а) Определение спектральной плотности входного импульса напряжения 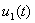 .
.
Спектральную плотность импульса напряжения 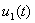 определяют с помощью прямого преобразования Фурье:
определяют с помощью прямого преобразования Фурье:
 (4.13)
(4.13)
АЧХ: 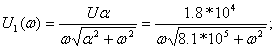
ФЧХ: 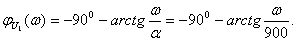 (4.14)
(4.14)
2) Определение комплексной передаточной функции по напряжению 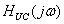
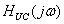 находят по формуле:
находят по формуле: 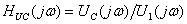 . Будем считать, что на вход цепи подано синусоидальное напряжение, комплексное действующее значение которого
. Будем считать, что на вход цепи подано синусоидальное напряжение, комплексное действующее значение которого 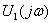 . Применяя комплексный метод расчёта (см. рисунок 4.16), определяют
. Применяя комплексный метод расчёта (см. рисунок 4.16), определяют 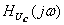 , АЧХ
, АЧХ 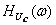 , ФЧХ
, ФЧХ 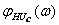 :
:
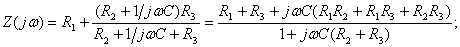
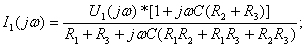
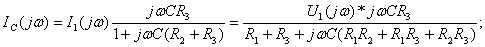
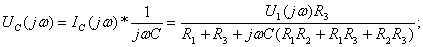
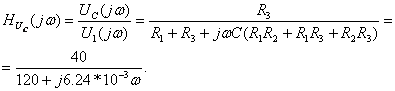 (4.15)
(4.15)
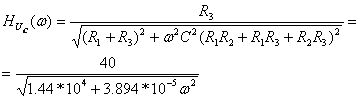 ,
,
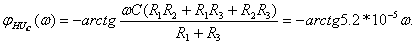
3) Определение спектральной плотности 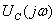 по спектру входного напряжения
по спектру входного напряжения 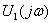 и соответствующей комплексной функции передачи
и соответствующей комплексной функции передачи 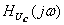 . Спектральную плотность реакции цепи
. Спектральную плотность реакции цепи 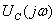 вычисляют по формуле
вычисляют по формуле 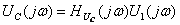 :
:
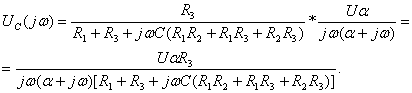 (4.16)
(4.16)
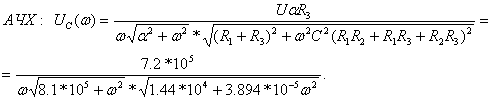
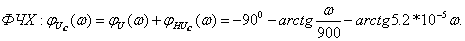
Графики АЧХ: 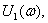
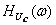 ,
, 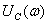 (см. рисунки 4.17, 4.19 4.21) и ФЧХ
(см. рисунки 4.17, 4.19 4.21) и ФЧХ 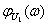 ,
, 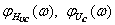 (см. рисунки 4.18, 4.20, 4.22) построены в среде Mathcad.
(см. рисунки 4.18, 4.20, 4.22) построены в среде Mathcad.

Рисунок 4.17 Рисунок 4.18
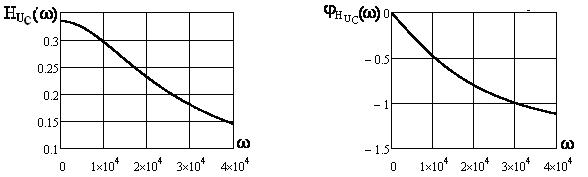
Рисунок 4.19 Рисунок 4.20
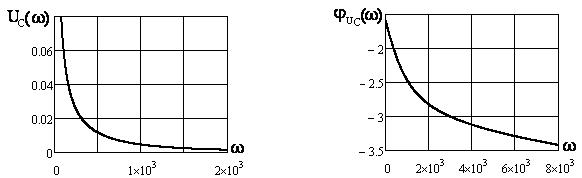
Рисунок 4.21 Рисунок 4.22
4) Определение реакции цепи 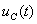 .
.
Реакцию цепи 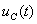 определяют по соответствующей спектральной плотности
определяют по соответствующей спектральной плотности 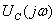 по теореме разложения. В выражении (4.15) заменяют
по теореме разложения. В выражении (4.15) заменяют 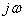 на р:
на р:
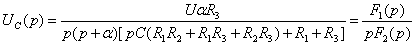 (4.17)
(4.17)
где 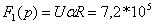 ,
,
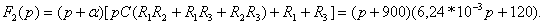 Находят корни характеристического уравнения
Находят корни характеристического уравнения  :
:
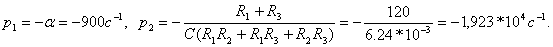
Реакцию цепи  определяют по теореме разложения:
определяют по теореме разложения:
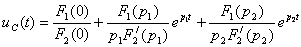 (4.18)
(4.18)
где 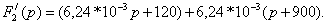
Рассчитывают:
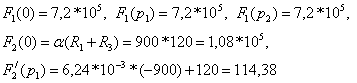
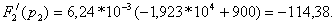
Подставляют полученные значения 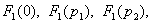
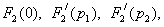 в выражение (4.18) и вычисляют реакцию цепи
в выражение (4.18) и вычисляют реакцию цепи 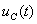 :
:
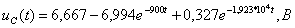 .
.
Ток 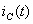 в ветви с ёмкостью находят по формуле:
в ветви с ёмкостью находят по формуле:
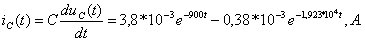
Графики  ,
,  (см. рисунки 4.23, 4.24) построены в среде Mathcad.
(см. рисунки 4.23, 4.24) построены в среде Mathcad.
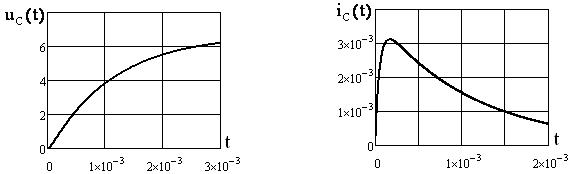
Рисунок 4.23 Рисунок 4.24
 2015-04-01
2015-04-01 4682
4682








