2015-04-01
7615
Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью l. Интенсивность потока обслуживания равна m (т. е. в среднем непрерывно занятый канал будет выдавать m обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.
Граф состояний СМО в этом случае имеет вид, показанный на рис. 5.2.
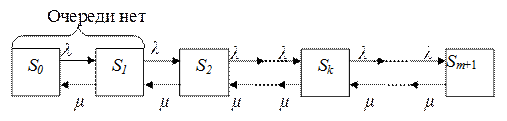
Рис. 5.2. Граф состояний одноканальной СМО с ожиданием
(схема гибели и размножения)
Состояния СМО имеют следующую интерпретацию:
S0 – «канал свободен»;
S1 – «канал занят» (очереди нет);
S2 – «канал занят» (одна заявка стоит в очереди);
Sk – «канал занят» (k-1 заявокстоит в очереди);
S m+1 – «канал занят» (m заявок стоит в очереди).
Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:
Пользуясь уравнениями для процесса гибели и размножения получим:
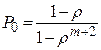(5.10)
где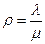 
– приведенная интенсивность (плотность) потока;
Тогда вероятность что занят 1 канал и k-1 мест в очереди:
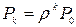
Следует отметить, что выполнение условия стационарности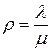 
< 1 для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать m), а не соотношением между интенсивностями входного потока, т. е. не отношением .
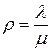Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной m:
вероятность отказа в обслуживании заявки;
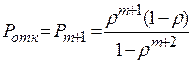; (5.11)
относительная пропускная способность системы:
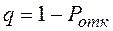; (5.12)
абсолютная пропускная способность:
А = ql; (5.13)
среднее число заявок, находящихся в очереди:
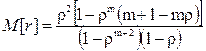; (5.14)
среднее число заявок, находящихся под обслуживанием:
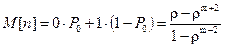(5.15)
среднее число заявок, находящихся в системе(связанных с СМО):
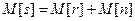; (5.16)
среднее время пребывания заявки в системе:
Тсист.= Тож. + tоб; (5.17)
средняя продолжительность пребывания клиента (заявки) в очереди:
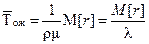. (5.18)
Если имеется неограниченное число мест ожидания в очереди m, то вышеуказанные формулы справедливы только при ρ < 1, так как при ρ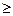 
1 нет установившегося режима (очередь неограниченно растет) и при 
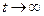q=1, A=λq=λ.
Рассмотрим пример одноканальной СМО с ожиданием.
Пример. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность l = 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.
Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Решение.
Интенсивность обслуживания автомобилей:
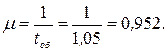(авто/час)
Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей l и m, т. е.
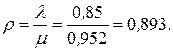
Вычислим предельные вероятности системы:
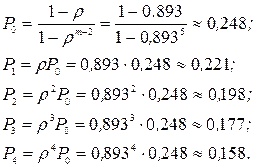
Вероятность отказа в обслуживании автомобиля:
Pотк = P4 = r4×P0» 0,158.
Значит 15,8% автомобилей получат отказ в обслуживании так как не будет свободных постов и мест в очереди.
Относительная пропускная способность поста диагностики:
q = 1 - Pотк= 1 - 0,158 = 0,842.
Это означает что обслуживается в среднем 82,4% автомобилей.
Абсолютная пропускная способность поста диагностики
А = lq = 0,85 × 0,842 = 0,716 (автомобиля в час).
Среднее число автомобилей, находящихся в системе – среднее число заявок, находящихся в очереди плюс среднее число заявок, находящихся под обслуживанием:
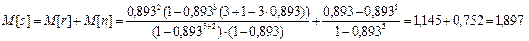
Среднее время пребывания автомобиля в системе складывается из среднего времени ожидания в очереди и продолжительности обслуживания (если заявка принята к обслуживанию):
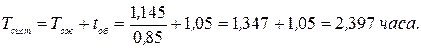
Работу рассмотренного поста диагностики можно считать удовлетворительной, так как пост диагностики не обслуживает автомобили в среднем в 15,8% случаев (Ротк = 0,158).
Задача 1. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой). Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 6). Если в очереди уже находится 6 машин, очередная машина, прибывшая к станции, в очередь не становится, а проезжает мимо. Поток машин, прибывающих для заправки, имеет интенсивность λ = 0,95 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин. Определить:
· вероятность отказа;
· относительную и абсолютную пропускную способности СМО;
· среднее число машин, ожидающих заправки;
· среднее число машин, находящихся на АЗС (включая и обслуживаемую);
· среднее время ожидания машины в очереди;
· среднее время пребывания машины на АЗС (включая обслуживание).
· доход АЗС за 10 часов при стоимости литра бензина равной 20 руб. и среднем объеме одной заправки автомобиля равной 7,5 литров.
Задача 2. Вспомним о ситуации, рассмотренной в задаче 1, где речь идет о функционировании поста диагностики. Пусть рассматриваемый пост диагностики располагает неограниченным количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.
Требуется определить финальные значения следующих вероятностных характеристик:
· вероятности состояний системы (поста диагностики);
· среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);
· среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);
· среднее число автомобилей в очереди на обслуживании;
· среднюю продолжительность пребывания автомобиля в очереди.
Задача 3. На железнодорожную сортировочную горку прибывают составы с интенсивностью λ = 2 (состава в час). Среднее время, в течение которого горка обрабатывает состав, равно 0,4 часа. Составы, прибывшие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеются три запасных пути, на каждом из которых может ожидать один состав. Состав, прибывший в момент, в очередь на внешний путь. Все потоки событий – простейшие. Найти:
· среднее число составов, ожидающих очереди (как в парке прибытия, так и вне его);
· среднее время ожидания состава в парке прибытия и на внешних путях;
· среднее время нахождения состава на сортировочной станции (включая ожидание и обслуживание);
· вероятность того, что прибывший состав займет место на внешних путях.
