2015-04-01
669
Если система имеет бесконечное множество решений, то все их перечислить невозможно. В этом случае строится общее решение системы.
Определение 7. Общим решением неопределенной системы называется такая система, эквивалентная исходной, в которой часть неизвестных, называемых зависимыми, выражена через остальные неизвестные, называемые независимыми.
Опишем способ нахождения общего решения системы, предполагая, что её матрица уже приведена к ступенчатому виду.
Пусть дана система 
.
1) Сначала надо выделить неизвестные. Которые будут зависимыми(остальные будут независимыми); для этого надо, обведя нули, нарисовать «лесенку», иллюстрирующую ступенчатый вид матрицы. Под теми столбцами, где начинаются «ступеньки» этой «лесенки» подписать неизвестные, соответствующие этим столбцам, и рядом написать букву «з». В данном примере это будет выглядеть так:
.
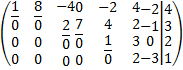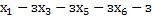
Выписанные неизвестные и будут считаться зависимыми.
2) Затем с помощью элементарных преобразований надо добиться, чтобы в столбцах соответствующих зависимым неизвестным, осталось лишь одно ненулевое число.
Делать это целесообразно двигаясь снизу вверх и справа на лево. В данном примере получим таким образом матрицу
.
3) Теперь надо систему из матричной формы записи перевести в обычную форму:
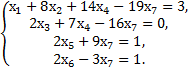
4) Выражая в каждом уравнении зависимую неизвестную, получаем общее решение системы:
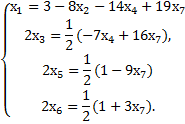
5) Теперь, придавая независимым неизменным произвольные значения и вычисляя зависимые, можно найти частное решение системы и сделать проверку.
В этом примере положим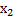 
=1, 
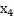=2,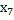 
=0, тогда 
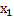=-33, 
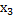=-7,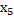 
= 
, 
= .
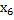Проверка. -33+8·1-4·(-7)-2· +4· -2·0=-33+8+28-1+2=4;
2(-7)+7·2+4· +2· -1·0=-14+14+2+1=3; +3 · =2; 2· -3· 0=1.
Замечание. Количество зависимых неизвестных должно равняться рангу матрицы.
