2015-04-01
3336
Пусть дана система m линейных уравнений с nнеизвестными общего вида
(*)
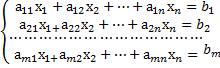Или в матричной форме, AX=b,
Где А = 
– матрица системы, размера mxn,
X =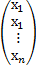 
– матрица-столбец неизвестных,
B =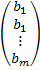 
– матрица-столбец свободных членов данной системы.
Определение 1. Решением системы называется такая совокупность n чисел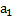 
, 
, …, 
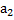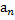, что при подстановке их во все уравнения системы вместо соответствующих неизвестных получаются числовые тождества.
Определение 2. Система, имеющая хотя бы одно решение, называется совместной; система, имеющая ни одного решения - несовместной.
Определение 3. Система, имеющая единственное решение, называется определенной; система, имеющая более одного решения - неопределенной.
Определение 4. Две системы называются эквивалентными, если множества их решений совпадают.
Определение 5. Матрица (Alb) = 
,
Получаемая из матрицы А системы добавлением столбца свободных членов, называется расширенной матрицей.
Теорема 1. Для того, чтобы система (*) была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы, т.е.
r(A)=(Alb).
Иначе, 1) r(A)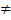 
r(Alb) 
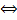система несовместна,
2)r(A)= r(Alb) 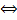система совместна,
3) r(A)= r(Alb) = n 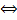система определенна,
4) r(A)= r(Alb)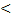 
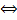n система неопределенна.
Алгоритм исследования произвольных система линейных уравнений методов Гаусса.
1) Сначала расширенная матрица (Alb) приводится с помощью элементарных преобразований к ступенчатому виду и матрица А системы (*));
2) затем находятся числа r(A), r(Alb) и n (n- число неизвестных системы);
3) проводится исследование системы согласно теоремы Кронекера-Капелли.
Пример 2. Исследовать систему.
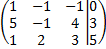
Решение.
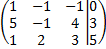= (2)-5(1) 
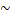(3)-(1) 
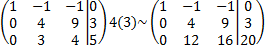(3)-3(2) 
(3) 
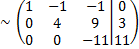
r(A)=3, r(Alb)=3, n=3.
Отве: система совместна и имеет единственное решение.
