2015-04-01
519
Определение 7. Линейными операциями над векторами называются сложение векторов и умножение вектора на число.
Определение 8. Суммой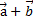 
двух векторов 
и 
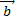называется вектор 
, который идет из начала вектора в конец вектора 
при условии, что вектор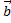 
приложен к концу вектора (правило треугольника). В случае неколлинеарных векторов и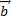 
можно вместо правила треугольника использовать правило параллелограмма: если векторы и отложены от общего начала и на них построен параллелограмм, то сумма 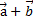есть вектор, совпадающий с диагональю этого параллелограмма, идущего из общего начала и .
Определение 9. Разностью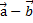 
двух векторов и называется вектор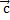 
, который в сумме с вектором составляет вектор . Если два вектора и отложены от общего начала, то их разность есть вектор, исходящий из конца вектора («вычитаемого») к концу вектора («уменьшаемого»).
Определение 10. Два коллинеарных вектора равной длины, направленные в противоположные стороны, называются противоположными. Вектор, противоположный вектору , обозначается 
.
|
|
|
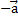Произведение вектора на число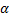 
обозначают α .
Некоторые свойства линейных операций
1) +(
)=( + )+ ;
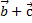2) = 
;
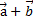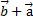3) 
+ 
= ;
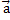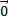4) +()= ;
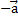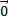5) 
= (
);
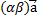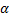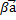6) 
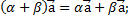
7) 
;
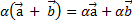8) 1· = .
Теорема 1. (О коллинеарных векторах). Если 
и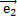 
– два коллинеарных вектора, причем вектор -ненулевой, то существует единственное число х такое, что 
=х
В частности, ненулевой вектор и его орт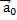 
связаны равенством: = 
· .
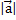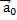Сформулированные свойства линейных операций позволяют преобразовать выражения, составленные из векторов, по обычным правилам алгебры: можно раскрыть скобки, приводить подобные члены, переносить некоторые члены в другую часть равенства с противоположным знаком и т.д.
