Системы n линейныйх алгебраических уравнений с n неизвестными
Пусть дана система nлинейных алгебраических уравнений с n неизвестными вида
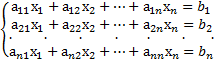
Или в матричной форме, АХ=b, где А=  –матрица системы,
–матрица системы,
X= 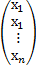 - матрица-столбец неизвестных,
- матрица-столбец неизвестных,
B = 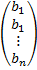 - матрица-столбец свободных членов данной системы.
- матрица-столбец свободных членов данной системы.
Правило Крамера
Если в системе detA 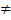 0, т.е. матрица А имеет обратную
0, т.е. матрица А имеет обратную 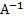 , то система имеет, и при этом единственное, решение X=
, то система имеет, и при этом единственное, решение X= 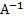 ·b, или
·b, или 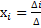 , i=1,2,…,n,
, i=1,2,…,n,
где 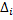 -определитель, получаемый из определителя
-определитель, получаемый из определителя  системы заменой i-го столбца на столбец свободных членов.
системы заменой i-го столбца на столбец свободных членов.
Пример 1. Решить систему уравнений по правилу Крамера
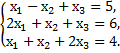
Решение.
Определитель системы  =
= 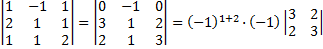 =5,
=5,
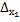 =
= 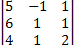 (2)+(1)=(3)+(1)=
(2)+(1)=(3)+(1)= 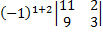 =15,
=15,
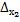 =
= 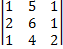 =1·
=1· 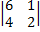 -5
-5 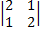 +1·
+1· 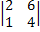 =8-15+2=-5;
=8-15+2=-5;
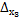 =
= 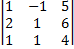 (2)+(1)=(3)+(1)
(2)+(1)=(3)+(1) 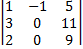 =(-1)·
=(-1)· 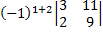 =5.
=5.
Тогда 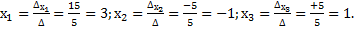
Ответ: 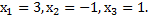
 2015-04-01
2015-04-01 864
864








