Векторное умножение обладает следующими четырьмя свойствами:
1)[  x
x  ]=-[
]=-[  х
х  ] (свойство антикоммутативности);
] (свойство антикоммутативности);
2) [(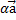 )х
)х  ]=
]= 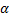 [
[  х
х  ] (свойство ассоциативности относительно числового множителя);
] (свойство ассоциативности относительно числового множителя);
3) [( +
+  )х
)х  ] = [(
] = [( x
x 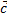 )]+[
)]+[  x
x 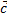 ] (свойство дистрибутивности относительно суммы векторов);
] (свойство дистрибутивности относительно суммы векторов);
4) [( х
х  )] =
)] =  для любого вектора
для любого вектора  .
.
Если  = {
= { 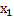 ;
; 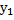 ;
; 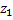 } и
} и  = {
= { 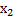 ;
; 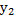 ;
; 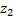 } – векторы, заданные своими координатами в пямоугольном базисе, то разложение векторного произведения [
} – векторы, заданные своими координатами в пямоугольном базисе, то разложение векторного произведения [  x
x  ] в том же базисе имеет вид:
] в том же базисе имеет вид:
[  x
x  ] =
] = 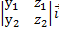 -
- 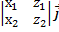 +
+ 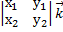 , или
, или  х
х  =
= 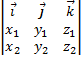 .
.
Пример 1. Доказать, что ( -
-  ) x (
) x ( +
+  ) = 2
) = 2  x
x  , и выяснить геометрическое значение этого тождества.
, и выяснить геометрическое значение этого тождества.
Решение.
( -
-  ) х (
) х ( +
+  ) =
) =  х
х  + (
+ ( х
х  ) – (
) – ( х
х  ) – (
) – ( х
х  ). Так как
). Так как  х
х  =
= 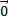 ,
,  х
х  =
= 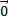 ,
,  х
х  = -[
= -[  х
х  ], то получаем
], то получаем
( -
-  ) x (
) x ( +
+  ) =2[
) =2[  x
x  ] и
] и 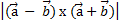 = 2
= 2 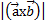 . Это с геометрической точки зрения означает: площадь параллелограмма, построенного на диагоналях данного параллелограмма, вдвое больше площади данного параллелограмма.
. Это с геометрической точки зрения означает: площадь параллелограмма, построенного на диагоналях данного параллелограмма, вдвое больше площади данного параллелограмма.
 2015-04-01
2015-04-01 793
793








