Векторное произведение векторов

Определение 1. Векторным произведением двух векторов и называют третий вектор , удовлетворяющий условиям:

1) 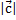= 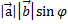, где-угол между и (0 );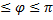

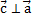2) вектор ортогонален векторам и , т.е. и ;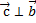

3)векторы , , образуют правую тройку векторов.

Векторное произведение векторов и обозначают х или [ x ].

Если хотя бы один из сомножителей равен 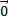, то векторное произведение по определению есть нулевой вектор.

Понятие векторного произведения родилось в механике. Если вектор = 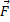изображает приложенную в некоторой точке Р силу, а вектор идет из некоторой точки О в точку Р, то вектор 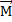=[ x ] = представляет собой момент силы 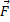относительно точки О.