1. Раскрыть скобки в выражении 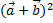 и выяснить геометрический смысл полученной формулы.
и выяснить геометрический смысл полученной формулы.
2. Даны три вектора 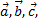 удовлетворяющие условию
удовлетворяющие условию 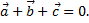 Зная, что
Зная, что 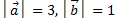 и
и 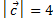 , вычислить
, вычислить 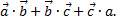
3. Векторы 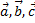 попарно образуют друг с другом углы, каждый из которых равен 60
попарно образуют друг с другом углы, каждый из которых равен 60  . Зная, что
. Зная, что 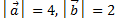 и
и 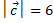 , определить модуль вектора
, определить модуль вектора 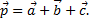
4. Какому условию должны удовлетворять векторы 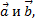 чтобы вектор
чтобы вектор 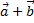 был ортогонален вектору
был ортогонален вектору 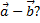
5. Доказать, что векторы 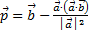 ортогонален вектору
ортогонален вектору 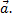
6. Даны векторы 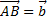 и
и 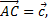 совпадающие со сторонами треугольника ABC. Найти разложение по базису
совпадающие со сторонами треугольника ABC. Найти разложение по базису 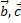 вектора, приложенного к вершине B этого треугольника и совпадающего с его высотой BD.
вектора, приложенного к вершине B этого треугольника и совпадающего с его высотой BD.
7. Даны векторы 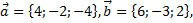 вычислить:
вычислить:
1) 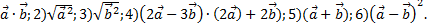
8. Дан равносторонний треугольник ABC, длины которого равны 1. Вычислить выражение 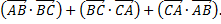
9. В треугольнике ABCданы длины его сторон: 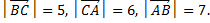 Найти скалярные произведения векторов
Найти скалярные произведения векторов 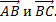
10. В треугольнике ABCпроведены медианы 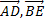 и
и 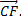 Вычислить
Вычислить 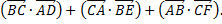
11. Найти скалярное произведение векторов 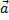 и
и 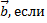
1) │ 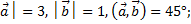
2) │ 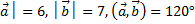
3) │ 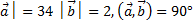
4) │ 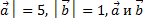 соноправлены;
соноправлены;
5) │ 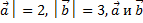 противоположно направлены.
противоположно направлены.
12. Вычислить выражение │ 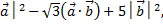 если:
если:
1) │ 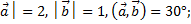
2) │ 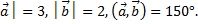
13. Найти скалярное произведение векторов 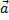 и
и  , заданных своими координатами:
, заданных своими координатами:
1) 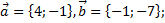
2) 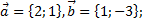
3) 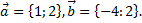
14. Найти расстояние между точками Aи B, заданными своими координатами:
1) 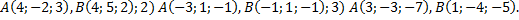
15. Даны три вектора: 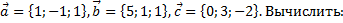
1) 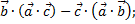
2) 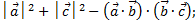
3) 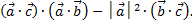
 2015-04-01
2015-04-01 1255
1255







