Пример: Вычислить определитель третьего порядка
Дана матрица размером 3х3;
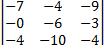
Что бы вычислить определитель матрицы 3х3 нужно воспользоваться формулой;
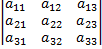 =
=
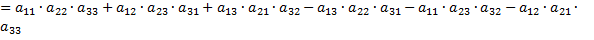
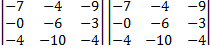
Подставляем наши значения в формулу;
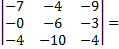
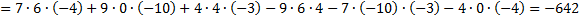
Ответ: -642
Пример: Вычислить определитель четвертого порядка
Дана матрица размером 4х4;
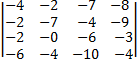
Есть два способа вычисления определителя матрицы:
1. По определению - через разложение по строке или столбцу;
2. По методу Гаусса - приведение матрицы к треугольному виду (этот способ лучше использовать для решения матриц, размером 4х4 и более).
Решим пример первым способом (по определению - через разложение по строке или столбцу)
Чтобы вычислить определитель матрицы, нужно воспользоваться следующей формулой, в ней рассмотрен пример разложения матрицы по первой строке;
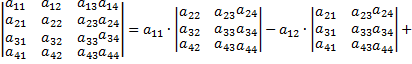
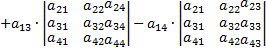
Итак, начнём
1. Выбираем строку или столбец (любую), лучше всего выбирать строку или столбец, где больше нулей, для удобства вычисления;
В данном случае мы выбираем третью строку, так как в ней присутствует ноль;
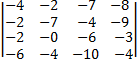
2. Берём первый элемент этой строки (2);
Теперь вычёркиваем третью строку и первый столбец;
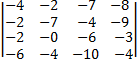
Получаем матрицу 3х3;
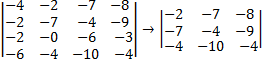
Согласно формуле, мы умножаем выбранный нами элемент на определитель получившейся матрицы;
Вычисление определителя матрицы 3х3, мы рассматривали в примере №2
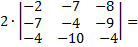
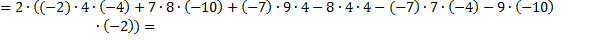
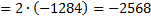
3. Далее делаем всё тоже самое, что и в шаге два, только берём второй элемент данной строки (0) и вычёркиваем третью строку и второй столбец;
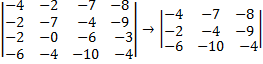
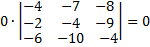
Так как этот элемент равен нулю, то ни чего не нужно считать и так всё ясно;
4. Теперь берём третий элемент строки (6) и вычёркиваем третью строку и третий столбец;
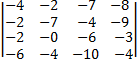
Получаем матрицу 3х3;
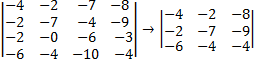
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (6)
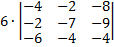 =
=
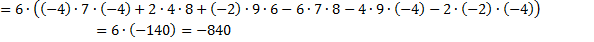
5. Берём четвёртый элемент строки (-3) и вычёркиваем третью строку и четвёртый столбец;
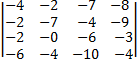
Получаем матрицу 3х3;
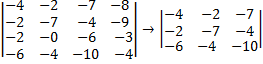
Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (-3)
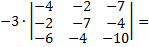
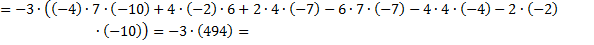
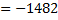
6. Чтобы вычислить определитель исходной матрицы, нужно сложить полученные результаты;
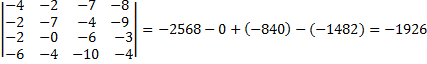
Ответ: -1926
Опишем решение примера вторым способом (по методу Гаусса - приведение матрицы к треугольному виду)
Суть способа заключается в том, чтобы перед вычислением определителя, привести матрицу к треугольному виду. Если в ходе приведения матрицы к треугольному виду вы умножаете (делите) строку на число, то на это же число нужно будет умножить (разделить) полученный в конце определитель;
Пример приведения матрицы к треугольному виду мы уже рассматривали
Итак, мы привили матрицу к треугольному виду;
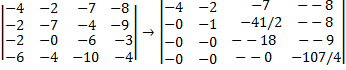
Теперь чтобы вычислить определитель приведённой матрицы, нужно перемножить все элементы, стоящие на главной диагонали;
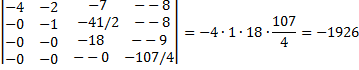
Ответ: -1926
Пример:
Перемножить матрицы:
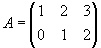 - размером (2 х 3)
- размером (2 х 3)
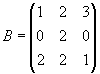 - размером (3 x 3)
- размером (3 x 3)
Решение:
Так как число столбцов А(3) совпадает с числом строк В (3), следовательно, можно их перемножить.
Чтобы получить элемент С11 произведения, умножим первую строку матрицы А на первый столбец матрицы В.
С11 = 1·1 + 2·0 + 3·2 = 7,
С12 получится умножением первой строки А на второй столбец В:
С12 = 1·2 + 2·2 +3·2 = 12
С13 – умножением первой строки А на третий столбец В:
С13 = 1·3 + 2·0 + 3·1 = 6
С21 –умножением второй строки А на первый столбец В:
С21 = 0·1 = 1·0 +2·2 = 4
Далее, умножая вторую строку А на второй столбец В, получим С22 =6, умножая вторую строку А на третий столбец В, получим С23 =2
Больше у нас строк нет. Получилась матрица С, состоящая из двух строк и трех столбцов
Пример:
Найдем обратную матрицу к матрице A
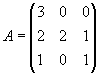
Как видно из формулы А-1, нам придется делить на определитель А, поэтому важно, а не окажется ли он равен нулю? Разложим А по первой строке, это нам удобно, т.к. там много нулей.
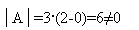
Определитель нулю не равен, значит обратная матрица существует.
Найдем алгебраические дополнения (знаки их учтем сразу) то есть 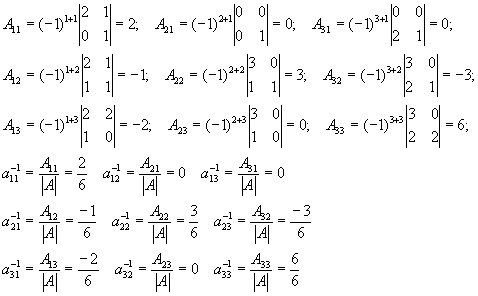
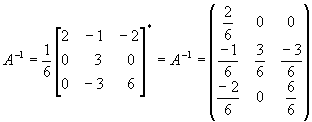
 2015-04-01
2015-04-01 3211
3211








