При условии доброжелательности игрок 2 оптимальный выигрыш игрока 1 в игре 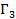 равен
равен 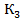 , а
, а 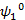 – его оптимальная стратегия.
– его оптимальная стратегия.
Доказательство.
Аналогично доказательству теоремы 1.
Замечание 1 и 2 к теореме 1 справедливы и для теоремы 2.
Кроме того, в силу 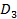 ≤
≤ 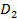 имеем
имеем 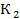 ≥
≥ 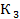 , то есть выигрыш игрока 1 в игре
, то есть выигрыш игрока 1 в игре 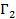 больше или равен его выигрышу в игре
больше или равен его выигрышу в игре 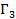 .
.
Упражнение.
Докажите, что если в антагонистической игре 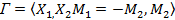 ,
,
существует седловая точка, то 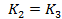
Пример.
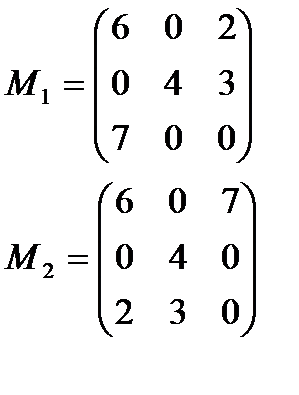
Ранее на этом примере, мы строили ситуации равновесия на сложных стратегиях. Теперь проиллюстрируем решение иерархических игр.
Игра 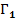
Определим множества рациональных ответов игрока 2.
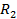 (1) = 3,
(1) = 3, 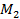 (1,3) = 7,
(1,3) = 7, 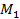 (1,3) = 2
(1,3) = 2
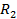 (2) = 2,
(2) = 2, 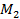 (2,2) = 4,
(2,2) = 4, 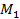 (2,2) = 4
(2,2) = 4
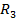 (3) = 2,
(3) = 2, 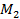 (3,2) = 3,
(3,2) = 3, 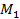 (3,2) = 0
(3,2) = 0
Тогда
max min 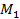 (
(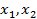 ) = max [2,4,0]=4
) = max [2,4,0]=4
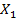 ={1,2,3}
={1,2,3} 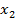
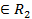 (
(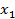 )
) 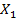 ={1,2,3},
={1,2,3},
при 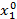 =2,
=2, 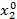 =2
=2
 2015-04-01
2015-04-01 392
392








