Теорема 1

При условии доброжелательности, оптимальный выигрыш игрока 1 в игре Г_2,равен К_2, а 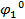( 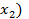- его оптимальная стратегия.

Доказательство:

При известной стратегии 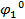( 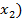игрок 2 получит:

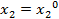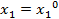- если , то и .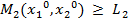

- если же игрок 2 выберет 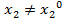, то его выигрыш не превысит

.

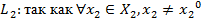
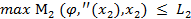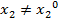
Если 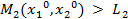, то множество R₂ (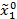) состоит из единственной точки .

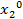В случае 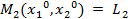множество R₂ (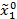) содержит выборы x₂ , в том числе 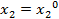, эквивалентные для игрока 2_. В силу доброжелательности игрока 2, он выберет точку 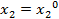- выгодную для игрока 1_.

Итак, в условиях теоремы игроку1 гарантируется исход 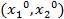, приводящий к выигрышу =

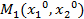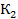
Покажем, что К₂ - максимальный гарантированный выигрыш.

Действительно, если исход (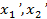) приводит к () > _,

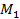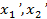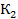то он лежит вне множества D₂ по определению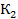

Но вне множества D₂ выигрыш игрока 2 оценивается величиной

() .

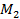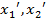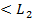Это не выгодно игроку 2 и он всегда может выбором 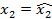получить _.

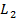Теорема доказана.