Иерархическая игра определяется следующими правилами (предполагается, что игрок 1 – начальник, игрок 2 – подчиненный):
1) Игрок 1 знает все параметры модели игрока 2, то есть множество 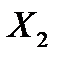 и функцию выигрыша
и функцию выигрыша 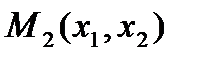 .
.
2) Игрок 1 делает свой ход первым, то есть выбирает стратегию 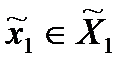 и сообщает информацию о ней игроку 2.
и сообщает информацию о ней игроку 2.
3) Игрок 2 при известной ему стратегии 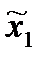 выбирает
выбирает 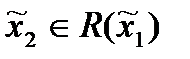 , то есть максимизирует свой критерий.
, то есть максимизирует свой критерий.
4) При наличии неопределенных факторов (в данном случае – неоднозначного выбора 2-го игрока из множества 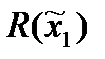 ) игрок 1 действует исходя из ОП МГР (4), а в случае доброжелательности игрока 2 в соответствии с (6).
) игрок 1 действует исходя из ОП МГР (4), а в случае доброжелательности игрока 2 в соответствии с (6).
На основании этих предположений в зависимости от информации о выборах 2-го игрока, которую игрок 1 имеет или ожидает иметь, формулируются разные игры. Рассмотрим их.
I. Игра 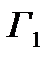 . В этой игре:
. В этой игре: 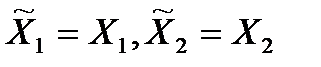 , то есть ни один из игроков заранее не знает о выборе другого. Здесь игрок 1 выбирает
, то есть ни один из игроков заранее не знает о выборе другого. Здесь игрок 1 выбирает 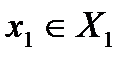 и сообщает об этом игроку 2, а он в свою очередь выбирает
и сообщает об этом игроку 2, а он в свою очередь выбирает 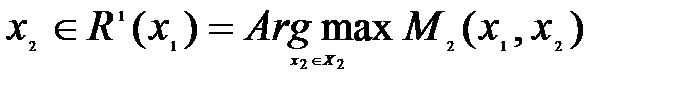 (множество точек, которое доставляет максимум функции
(множество точек, которое доставляет максимум функции 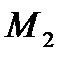 )
)
Тогда в этой игре МГР 1-го игрока:
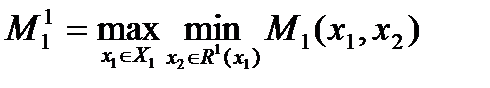
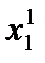 - оптимальное управление (стратегия), определяемая условием:
- оптимальное управление (стратегия), определяемая условием:
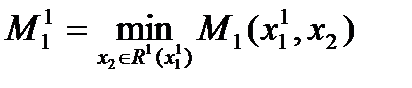
В случае доброжелательности игрока 2 МГР игрока 1 равен
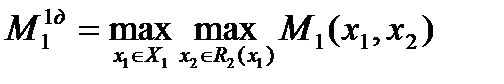 ,
,
а оптимальная стратегия определяется из условия
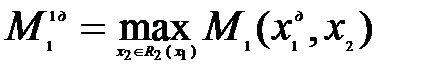
Можно «стимулировать» доброжелательность, используя побочный платеж 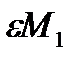 . В этом случае, функция выигрыша игрока 2 примет вид:
. В этом случае, функция выигрыша игрока 2 примет вид:
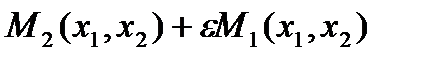
Аналогичный прием можно использовать в играх 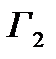 и
и 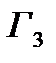 (смотри далее).
(смотри далее).
II. Игра 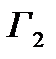 . В этой игре
. В этой игре 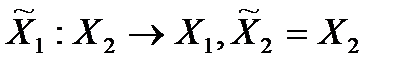 , то есть игрок 1 перед выбором своей стратегии будет знать выбор игрока 2. Таким образом, стратегия 1-го игрока выглядит следующим образом:
, то есть игрок 1 перед выбором своей стратегии будет знать выбор игрока 2. Таким образом, стратегия 1-го игрока выглядит следующим образом:
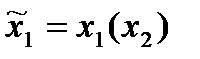
III. Игра 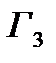 . В этой игре
. В этой игре 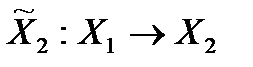 , то есть игрок 2 перед выбором
, то есть игрок 2 перед выбором 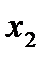 знает
знает 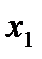 . Стратегия 2-го игрока:
. Стратегия 2-го игрока:
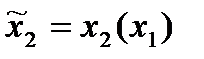
Однако первый игрок знает правило поведения 2-го (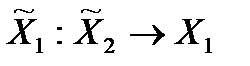 ) и поэтому его стратегия будет такой:
) и поэтому его стратегия будет такой:
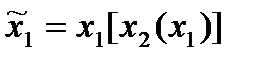
Замечание 5.
В играх 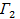 и
и 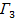 оптимальный выигрыш 1-го игрока определяется формулой (4). Таким образом, решение игр
оптимальный выигрыш 1-го игрока определяется формулой (4). Таким образом, решение игр 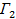 и
и 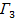 сводится к вариационным и более сложным задачам. Однако далее мы конструктивно определим решение этих игр на исходном множестве управлений
сводится к вариационным и более сложным задачам. Однако далее мы конструктивно определим решение этих игр на исходном множестве управлений 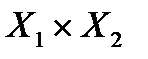 .
.
Замечание 6.
Можно рассматривать игры 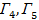 ,
, 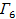 ,. ..
,. .. 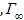 . Но оказывается, что ситуация 4 сводится к ситуации 2, ситуация 5 сводится к ситуации 3, а ситуация 6 сводится к ситуации 4 и т.д., то есть;
. Но оказывается, что ситуация 4 сводится к ситуации 2, ситуация 5 сводится к ситуации 3, а ситуация 6 сводится к ситуации 4 и т.д., то есть;
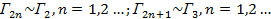
Из этого следует, что просчет вариантов действий в глубину не следует делать больше трех, дальше все повторяется.
Экономическая интерпретация иерархических игр Г1, Г2 и Г3
Игра 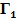 . Эта игра моделирует процесс управления ценами на произведенную продукцию и затрачиваемые ресурсы:
. Эта игра моделирует процесс управления ценами на произведенную продукцию и затрачиваемые ресурсы:
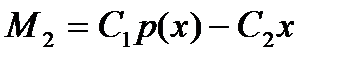
где x – ресурс,
p(x) – продукция,
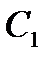 - цена на продукцию,
- цена на продукцию,
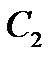 - цена на ресурс.
- цена на ресурс.
Пусть 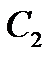 фиксирована.
фиксирована.
Найти 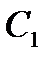 такую, что
такую, что 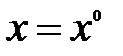 было выгодно игроку 2.Из необходимого условия экстремума имеем:
было выгодно игроку 2.Из необходимого условия экстремума имеем:
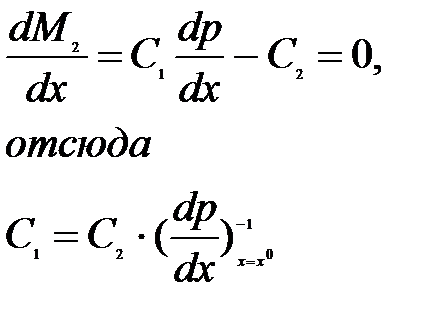
Если 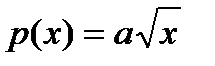 , то
, то
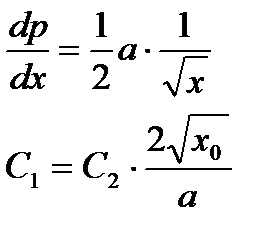 ,
,
Игра 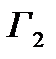 . Эта игра моделирует процесс управления штрафами, поощрениями.
. Эта игра моделирует процесс управления штрафами, поощрениями.
Опять пусть
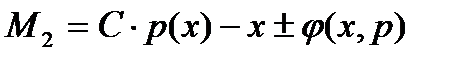
«+» - премия, «-» - штраф, налог.
Тогда стимулирование выбора 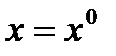 можно, например, произвести следующим образом (для определенности
можно, например, произвести следующим образом (для определенности 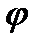 - штраф)
- штраф)
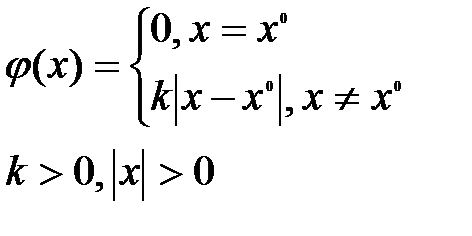
Игра 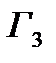 . Эта игра моделирует процесс выдачи ресурсов, кредитования под обоснованную программу их использования
. Эта игра моделирует процесс выдачи ресурсов, кредитования под обоснованную программу их использования
Пусть игрок 1 стимулирует реализацию ситуации 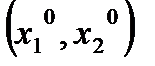 . Тогда он должен стимулировать игрока 2 выбрать программу
. Тогда он должен стимулировать игрока 2 выбрать программу 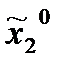 использования выделяемого ресурса:
использования выделяемого ресурса:
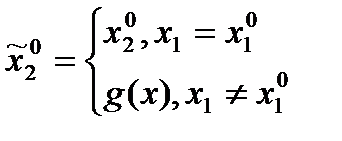
где 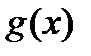 - произвольная функция.
- произвольная функция.
Игроку 1 важно только, что выделяемый ресурс 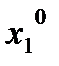 используется игроком 2 следующим образом
используется игроком 2 следующим образом 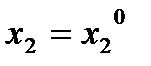 . Поэтому оптимальная стратегия игрока 1 имеет вид
. Поэтому оптимальная стратегия игрока 1 имеет вид
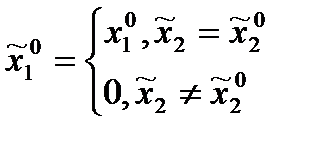
Как уже
Решение игр 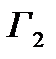 и
и 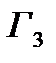 сводится к вариационным и более сложным задачам. Однако далее мы конструктивно определим решение этих игр на исходном множестве управлений
сводится к вариационным и более сложным задачам. Однако далее мы конструктивно определим решение этих игр на исходном множестве управлений 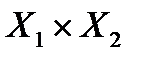 .
.
Игра Г2.
В этой игре 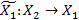 , т.е. игрок 1 до выбора
, т.е. игрок 1 до выбора
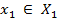 имеет информацию о
имеет информацию о 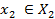 .
.
Поэтому стратегии игрока 1 – функции
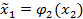
Для игрока 2 имеем 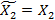
Вспомогательные конструкции.
Стратегия наказания:
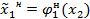 определяется из условия:
определяется из условия:
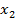
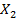
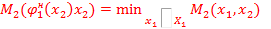
Максимально гарантированный результат (МГР) подчиненного равен
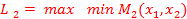
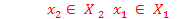
Множество исходов выгодное подчиненному
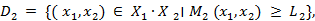
Исходы (x1, x2 ) вне этого множества не устраивают игрока 2 и он всегда может добиться выигрыша не меньше, чем L2 , выбирая x2 = xˆ2 из условия
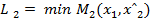
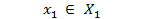
Определим 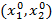 из равенства
из равенства 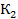
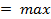
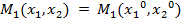
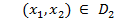
Наконец определим
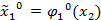 =
= 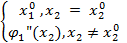
Отметим, что 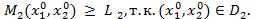
 2015-04-01
2015-04-01 2406
2406








