2015-04-01
311
Итак мы провели анализ элементарной ячейки иерархической системы управления (ИСУ). Сначала был рассмотрен вариант взаимодействия элементов, находящихся на одном уровне иерархии, затем – на разных уровнях.
В достаточно общей постановке анализ двухуровневой статической модели ИСУ сводится к решению игры n+1 лица, определяемой следующими параметрами:
1⁰ Задано множество игроков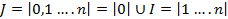 
.
Подмножества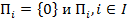 
определяют верхний и нижний уровни иерархии. Центр (Игрок 
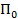) обладаем правом первого хода, т.е. первым выбирает и сообщает свою стратегию элементу нижнего уровня 
.
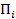2⁰ Вектора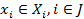 
определяют управляющие параметры . 
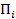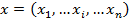набор управлений всех элементов нижнего уровня, 
.
3⁰ На множестве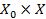 
заданы целевые функции:
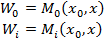
Интересы 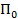описываются стремлением к максимизации этих функций.
4⁰ Взаимная информированность 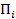соответствует порядку ходов и определяет их стратегии 
.
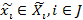5 
Для ,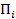 
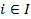определены правила поведения (принципы оптимальности), которые позволяют центру 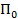оценить множество возможных ответов элементов нижнего уровня: 
.
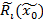Сформулированная игра многих лиц является обобщением игр двух лиц, рассмотренных ранее. Исследование значительно упрощается, если модель ИСУ имеет веерную структуру.
ИСУ называется веерной, если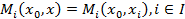 
. Функции выигрыша элементов нижнего уровня таких ИСУ зависят от управления центра и своего управления и не зависят от управлений своих соседей.
Задача рассматривается в интересах центра. Рассмотрим данный тип игр на примере игр, аналогичных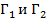 
.
1. Аналог игры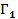 
Правило 1.1 В этом случае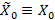 
, т.е. центр не имеет информации о действиях подчиненного до своего выбора.
Правило 1.2 Для любого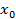 
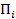выбирает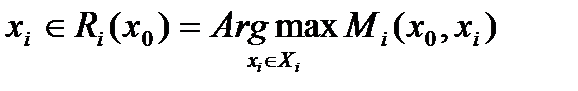 
Правило 1.3 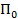выбирает 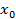из условия МГР.
Правила 1.1-1.3 получены путем конкретизации параметров 1⁰-5⁰ игры общего вида.
