Условие доброжелательности может быть опущено, если множество 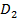 является замыканием не пустого множества
является замыканием не пустого множества
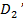 = {(
= {(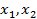 )
) 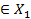 ×
× 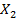 |
| 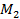 (
(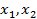 ) >
) > 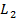 }
}
Действительно, в этом случае даже, если 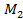 (
(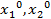 ) = L2, можно «скорректировать» оптимальную стратегию, заменив ее стратегией
) = L2, можно «скорректировать» оптимальную стратегию, заменив ее стратегией
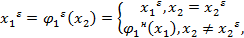
Где точка (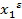 ,
, 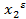 ) удовлетворяет условиям:
) удовлетворяет условиям:
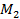 (
(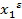 ,
, 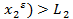
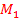 (
(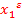 ,
, 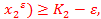
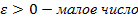 ,
,
величина 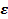 определяет затраты игрок 1 на стимуляцию игрока 2.
определяет затраты игрок 1 на стимуляцию игрока 2.
Механизмом такой стимуляции может служить «побочный платеж».
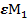 (
(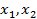 ) обещанный начальником подчиненному.
) обещанный начальником подчиненному.
Игра 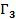
В этой игре игрок 2 знает выбор игрока 1 до своего выбора 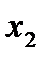 , т.е.:
, т.е.: 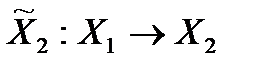 ,
, 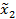 =
= 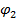 (
(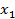 ). В свою очередь игрок 1 знает такое правило поведения игрока 2, т.е.
). В свою очередь игрок 1 знает такое правило поведения игрока 2, т.е. 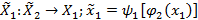
Вспомогательные конструкции.
Определим МГР игрока 2:
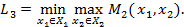
Далее определим стратегию наказания (стратегию наихудшую для игрока 2)
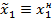
из условия
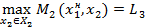
В игре 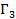 взаимовыгодное множество
взаимовыгодное множество 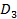 определяется равенством
определяется равенством
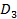 = {(
= {(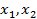 )
)
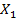 ×
× 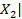
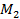 ≥
≥ 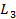 }
}
Напомним, что всегда 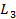 ≥
≥ 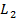 , поэтому
, поэтому 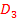
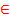
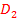 . Определим исход (
. Определим исход (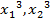 ) из условия
) из условия
К3 = 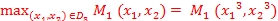
Построим стратегию игрока 2:
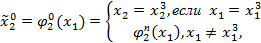
где 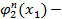 произвольная функция.
произвольная функция.
Оптимальная стратегия игрока 1имеет вид:
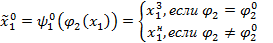
Содержательно игрок 1 выберет 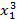 (выдает кредит), если игрок 2 использует этот кредит выбором
(выдает кредит), если игрок 2 использует этот кредит выбором 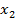 =
= 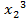 ,при этом игрок 2 получает
,при этом игрок 2 получает 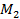 (
(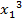 ,
, 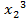 ) ≥
) ≥ 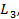
В противном случае игрок 1 выбирает 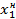 и игрок 2 не получит больше
и игрок 2 не получит больше 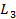 .
.
 2015-04-01
2015-04-01 366
366








