Пример 1. Найти все собственные числа и собственные векторы для линейного оператора с матрицей А:
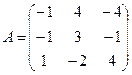 .
.
Найдём характеристическое уравнение.
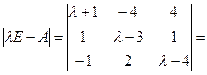
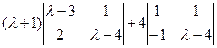
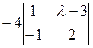 =
= 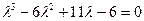 .
.
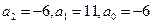 . Число –6 делится без остатка на 1,2,3 и 6.Тогда p может принимать значения 1,2,3, 6. q = +1 или –1. Поэтому среди рациональных чисел корни могут быть только +1,-1,+2,-2,+3, -3, 6,-6. Находим 3 характеристических корня: 1,2 и 3. Далее, решаем однородную систему уравнений
. Число –6 делится без остатка на 1,2,3 и 6.Тогда p может принимать значения 1,2,3, 6. q = +1 или –1. Поэтому среди рациональных чисел корни могут быть только +1,-1,+2,-2,+3, -3, 6,-6. Находим 3 характеристических корня: 1,2 и 3. Далее, решаем однородную систему уравнений 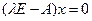 для каждого из трёх собственных чисел.
для каждого из трёх собственных чисел.
1) 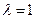 .
.
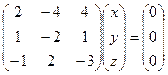
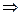
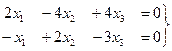
(ранг системы равен 2, рассматриваем 1-е и 3-е уравнения). Первый и второй столбцы не образуют базисный минор, поэтому 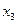 не может быть свободной переменной. Пусть свободной переменной будет
не может быть свободной переменной. Пусть свободной переменной будет 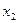 , и далее, решая систему, получаем фундаментальную систему решений: вектор
, и далее, решая систему, получаем фундаментальную систему решений: вектор 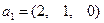 .
.
Проверка: умножаем матрицу оператора на этот вектор и видим, что он действительно является собственным и соответствует 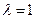 :
:
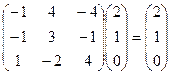 .
.
2) 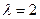 .
.
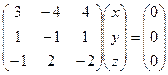
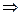
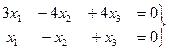
Здесь фундаментальная система решений – вектор 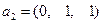 .
.
Проверка: 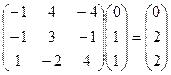
3) 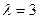 .
.
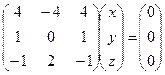
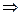
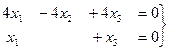
здесь фундаментальной системой решений будет 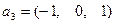 .
.
Проверка: 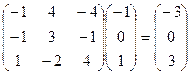 .
.
 2015-04-01
2015-04-01 920
920








