2015-04-01
965
= 
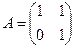
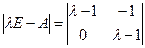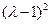= 0, характеристический корень равен 1, его кратность равна двум. Однако для этого линейного оператора не существует линейно-независимой системы из двух собственных векторов на плоскости. Решаем однородную систему, получающуюся при подстановке значения 
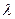=1.
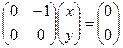
Второе уравнение будет тождеством 0 = 0, первое уравнение: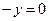 
, при этом x – свободная неизвестная, отсюда следует, что собственным вектором будет вектор (1,0). Базисный минор в этом примере - первого порядка, то есть, несмотря на то что корень кратности 2, ранг матрицы при подстановке характеристического корня понижается на единицу. Поэтому в системе одна свободная переменная, и один собственный вектор.
