Все характеристические корни действительны, но среди них есть кратные

Количество линейно-независимых собственных векторов для кратного корня совпадает с его кратностью.

Пример. Найти собственные числа и собственные векторы для линейного оператора, заданного матрицей:

.

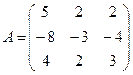
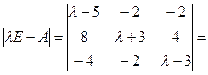
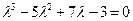Число 1 является корнем данного многочлена, затем делим на 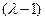и находим ещё два корня. Итак, собственными числами будут 1, 1 и 3. Корень 1 имеет кратность 2. При его подстановке вместо 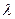, получим матрицу ранга 1, то есть все 3 строки оказываются линейно зависимыми. Тогда фундаментальная система решений состоит из двух векторов.

1) .

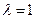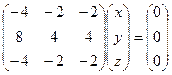
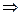
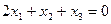, свободные переменные 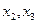, фундаментальная система решений:

,

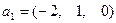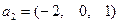
1) .

,

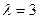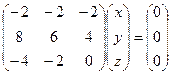
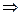
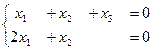фундаментальная система решений:

.

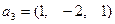Проверку можно провести аналогично предыдущему примеру.