Не все характеристические корни действительны

Для действительных корней собственные векторы находятся рассмотренными ранее способами. Однако собственных векторов будет меньше чем n. Если характеристический многочлен – чётной степени, и для него нет ни одного действительного корня, то собственные векторы отсутствуют. Так, например, для оператора поворота на угол 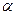, задаваемого матрицей:

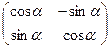
нет ни одного собственного вектора, кроме тех случаев, когда угол поворота 0⁰ или 180⁰.

Если линейное пространство нечётной размерности, то всегда существует хотя бы один собственный вектор. Так как для линейного оператора в пространстве нечётной размерности характеристический многочлен будет нечётной степени, то для него обязательно существует хотя бы один корень. Отсюда следует, что существует собственный вектор.

В частности, именно этим фактом объясняется, что при вращении сферы (в трёхмерном пространстве, нечётной размерности) обязательно есть ось (прямая, переходящая в себя при повороте на любой угол) и 2 полюса (точки на поверхности, остающиеся неподвижными). А при вращении круга (на плоскости, то есть в двумерном пространстве, размерность - чётная) ни одна точка, кроме 0, не остаётся на той же самой прямой.