Матрица линейного оператора в новом базисе вычисляется по формуле 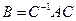 , где
, где 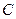 - матрица перехода от старого базиса к новому. Особый интерес представляет тот случай, когда новый базис или полностью, или хотя бы частично состоит из собственных векторов линейного оператора. При этом строение матрицы линейного оператора сильно упрощается, а если все n векторов базиса – собственные векторы, то матрица будет диагональной, причём по диагонали расположены n собственных чисел. Допустим, что
- матрица перехода от старого базиса к новому. Особый интерес представляет тот случай, когда новый базис или полностью, или хотя бы частично состоит из собственных векторов линейного оператора. При этом строение матрицы линейного оператора сильно упрощается, а если все n векторов базиса – собственные векторы, то матрица будет диагональной, причём по диагонали расположены n собственных чисел. Допустим, что 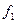 - собственный вектор, соответствующий собственному числу
- собственный вектор, соответствующий собственному числу 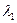 . Тогда этот вектор отображается оператором в вектор
. Тогда этот вектор отображается оператором в вектор 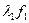 , то есть
, то есть 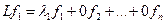 . Это и означает, что первый столбец матрицы оператора состоит из чисел
. Это и означает, что первый столбец матрицы оператора состоит из чисел 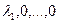 . Аналогично
. Аналогично 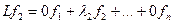 , то есть во втором столбце - все нули кроме элемента
, то есть во втором столбце - все нули кроме элемента 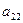 , который равен собственному числу
, который равен собственному числу 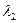 . Таким же образом для остальных столбцов получается, что единственный ненулевой элемент столбца будет расположен на диагонали матрицы. Если все n векторов базиса – собственные, то матрица оператора диагональная, а если только первые m векторов собственные, то только в первых m столбцах все элементы кроме диагональных будут нулевые.
. Таким же образом для остальных столбцов получается, что единственный ненулевой элемент столбца будет расположен на диагонали матрицы. Если все n векторов базиса – собственные, то матрица оператора диагональная, а если только первые m векторов собственные, то только в первых m столбцах все элементы кроме диагональных будут нулевые.
3.5. Построение матрицы оператора по известным собственным числам и векторам. (Обратная задача к задаче о нахождении собственных векторов). Если известно n собственных чисел и n собственных векторов, можно однозначно определить матрицу оператора, для которого данные числа и векторы будут собственными.
Доказательство. Пусть новый базис состоит из собственных векторов линейного оператора. Матрицу перехода от старого базиса к этому базису обозначим 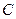 . Верна формула
. Верна формула 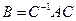 , где
, где 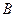 - матрица оператора в новом базисе, она является диагональной и содержит n собственных чисел по диагонали. Умножая это матричное равенство справа на
- матрица оператора в новом базисе, она является диагональной и содержит n собственных чисел по диагонали. Умножая это матричное равенство справа на 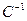 , а слева на
, а слева на 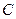 , получим формулу для вычисления матрицы оператора:
, получим формулу для вычисления матрицы оператора: 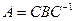 .
.
Пример. Найти матрицу линейного оператора, для которого собственными числами являются 1, 2 и 3, а собственными векторами соответственно 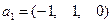 ,
, 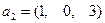 ,
, 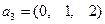 .
.
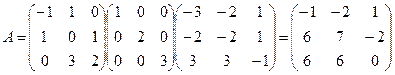 .
.
В §5 приведены варианты задач по теме «собственные числа и векторы».
В задачах (1-90) есть 3 различных характеристических корня. В задачах (91-180) есть один корень кратности 2. Во всех задачах корни – целые действительные числа.
 2015-04-01
2015-04-01 6555
6555
