Для чистых мод плоских упругих волн, распространяющихся вдоль одной из координатных осей, из выражения (32) для компонент вектора Умова, опуская индексы, будем иметь

Под T и u здесь следует понимать выраженные в комплексном виде чисто продольные, либо чисто поперечные волны напряжения и смещения. Сопоставим фрмулу (36) с выражением для мощности, переносимой электромагнитной волной, в некоторой передающей линии

где электрическое напряжение V и ток J в общем случае обусловлены суммой прямых и обратных волн. Сравнение формул (36) и (37) позволяет сделать вывод, что плоскую волну величины (- du/dt) можно принять аналогом волны электрического тока J, а волну упругого напряжения T - аналогом волны электрического напряжения. Это дает основание подобно электрическому импедансу в некотором сечении передающей линии ввести понятие акустического импеданса
 В общем случае, когда в среде одновременно присутствуют прямые и обрат-ные акустические волны, импеданс Z ак будет комплексной величиной, зависящей от координаты вдоль звукопровода. Если же имеют место чисто бегущие волны, то эта величина становится действительным числом, называемым акустическим волновым сопротивлением Z 0,ак.
В общем случае, когда в среде одновременно присутствуют прямые и обрат-ные акустические волны, импеданс Z ак будет комплексной величиной, зависящей от координаты вдоль звукопровода. Если же имеют место чисто бегущие волны, то эта величина становится действительным числом, называемым акустическим волновым сопротивлением Z 0,ак.

где знак + означает прямую бегущую волну. Для пьезоэлектрика из (28) и (29) имеем
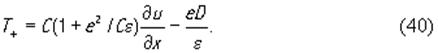
Здесь индукция D, как следует из (30), не зависит от координаты x и поэтому может быть функцией только времени D=D0e jωt. Если же пьезоэлектрик используется как простой звукопровод и не включен в какую-либо электрическую цепь, то ток в нем должен отсутствовать, т.е ∂ D /dt = jω D = O. На этом основании, полагая в (40) D =O и подставляя в (39), для бегущей волны получим 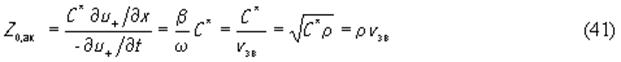
где C* =C(1+k2) - ужесточенная за счет пьезоэффекта упругая кoнстанта, k 2= e 2/ C ε - квадрат коэффициента электромеханической связи. Используя понятие акустического волнового сопротивления, можно плотность потока мощности, переносимой бегущей акустической волной, записать в виде
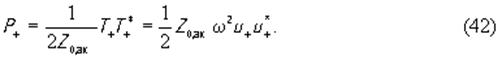
Понятие акустического импеданса широко используется при описании распространения плоских объемных упругих волн в различных контактирующих между собой средах. Так, например, если акустические волновые сопротивления двух сред равны, то при прохождении упругой волны из одной среды в другую не будет возникать отраженной волны. Если же некоторую среду с акустическим волновым сопротивлением Z0,ак соединить с другой средой, акустический импеданс которой равен Z ак, то в месте соединения комплексный коэффициент отражения будет равен

Также, как и в электромагнитных волноводах, акустический импеданс трансформируется отрезком звукопровода по закону
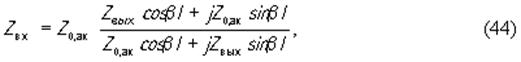
где Z вх, Z вых - акустические импедансы на входе и выходе трансформирующего отрезка длины l, β- пοстоянная распространения упругой волны. Для звукопроводов с потерями акустическое волновое сопротивление становится комплексным. Если
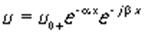
где α- коэффициент затухания, то из (39) следует

Эта формула может быть использована, например, для нахождения коэффициента акустического затухания α в некоторой среде по измеренному коэффициенту отражения от границы раздела между звукопроводом и исследуемой средой.
 2015-04-01
2015-04-01 1567
1567








