Определение. Функция F(x), определенная на некотором множестве называется первообразной для функции y=f(x) на этом множестве, если выполняется условие 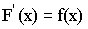
Определение. Если F(x)- одна из первообразных функции f(x), то множество функций вида F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом функции f(x) и обозначается 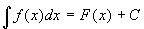 ,
,
где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение. Дифференциал в подынтегральном выражении указывает переменную интегрирования.
Действие нахождения первообразной называется интегрированием.
Свойства неопределенного интеграла.
1. 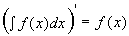
 3.
3. 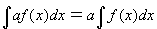 , где а=const
, где а=const
2. 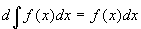 4.
4. 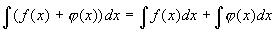
5. Если 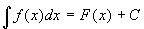 , то
, то 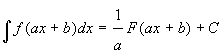
Основные формулы интегрирования.
1. 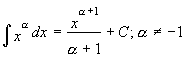 8.
8. 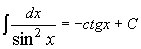
2. 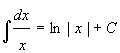 9.
9. 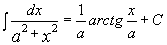
3. 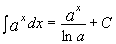 10.
10. 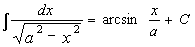
4. 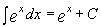 11.
11. 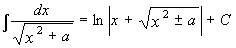
5. 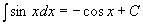 12.
12. 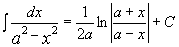
6. 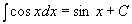 13.
13. 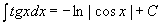
7. 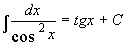 14.
14. 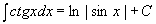
В этих формулах а – постоянная величина. Результаты интегрирования можно проверить дифференцированием.
 2015-04-06
2015-04-06 206
206







