Пусть функции U=U(x) и V=V(x) имеют на некотором промежутке непрерывные производные. Из формулы дифференциала произведения d(U•V)=UdV+VdU интегрированием обеих частей равенства получается формула интегрирования по частям
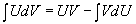
Эта формула дает возможность свести вычисления интеграла 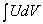 к вычислению интеграла
к вычислению интеграла 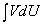 , который во многих случаях оказывается более простым. Рассмотрим два типа интегралов, которые вычисляются методом интегрирования по частям.
, который во многих случаях оказывается более простым. Рассмотрим два типа интегралов, которые вычисляются методом интегрирования по частям.
I. Интегралы вида,
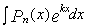 ,
, 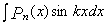 ,
, 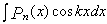 ,
,
где 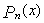 - алгебраический многочлен, k – некоторое число. Во всех интегралах обозначаем за
- алгебраический многочлен, k – некоторое число. Во всех интегралах обозначаем за 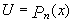 , а оставшееся выражение за dV, причем при нахождении V не записываем константу.
, а оставшееся выражение за dV, причем при нахождении V не записываем константу.
Примеры.
а) 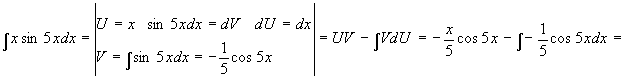
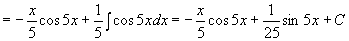
б) 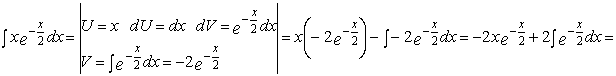
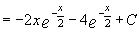
II. Интегралы вида.
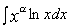 ,
, 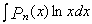 ,
, 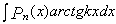 ,
, 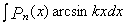 ,
,
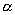 - действительное число.
- действительное число.
В этих случаях за U принимаем 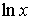 ,
, 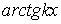 ,
, 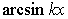 соответственно.
соответственно.
Примеры.
а) 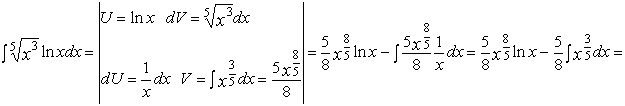
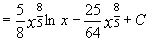
 2015-04-06
2015-04-06 278
278








