Определенный интеграл

Пусть на отрезке [a,b] задана некоторая функция. Разобьем этот отрезок на n частей, обозначая точки деления через

а = x₀ < x₁ < x₂ <…< x_n-1< x_n = b, а длины полученных промежутков

∆x₁ = x₁-x₀; ∆x₂ = x₂-x₁;… ∆x_n = x_n – x_n-1

В каждом из отрезков [x_i-1;x_i] выберем произвольную точку 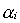, значение функции в выбранной точке 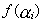умножим на длину соответствующего отрезка и составим сумму всех таких произведений:

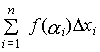
Полученная сумма называется интегральной. Пусть 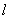- длина наибольшего из частных отрезков 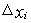. Если существует такое число 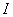, что интегральная сумма стремится к 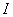при 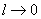и при любом выборе точек разбиения 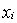и 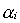, то это число 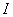называется определенным интегралом функции 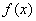на отрезке [a;b] и обозначается

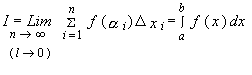
При введении понятия определенного интеграла существенными являются условия ограниченности функции 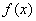на отрезке [a;b]. В частности, интегрируемыми являются непрерывные на отрезке функции, монотонные функции, кусочно-монотонные функции.

Основные свойства определенного интеграла.

1)

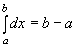
2) 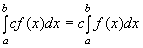, где с – некоторое число

3)

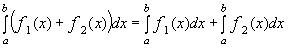
4)

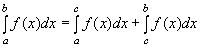
5)

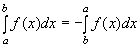
6)

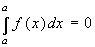
7) если 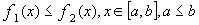, то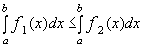

8) Если 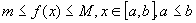, то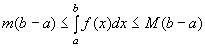

9) Если 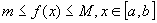, то существует число 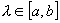такое, что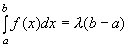

10)Если функция f(x) непрерывна на отрезке [a,b], то для любого переменного 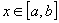существует интеграл 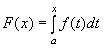и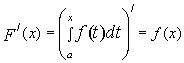

11)Если функция f(x) непрерывна на отрезке [a,b], F(x) – первообразная функции f(x), то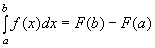

Данная формула называется формулой Ньютона-Лейбница и, обычно, записывается в виде: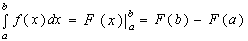

Если при вычислении определенного интеграла 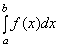от непрерывной функции 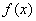требуется ввести новую переменную 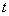, такую что 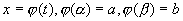, функция 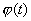дифференцируема на отрезке 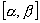, то

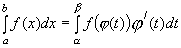
Изменение пределов позволяет не возвращаться по вычислении интеграла к первоначальной переменной х.

Есл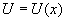и и 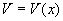- дифференцируемые на отрезке [a,b] функции, то формула интегрирования по частям для определенного интеграла имеет вид:

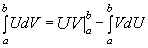
Примеры. Вычислить определенные интегралы.

1)

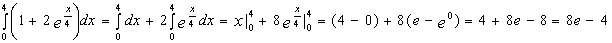
2)

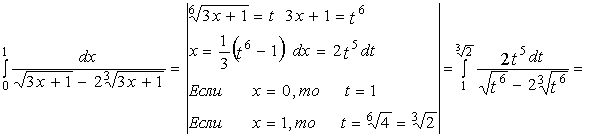
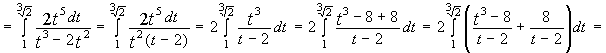
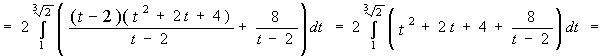
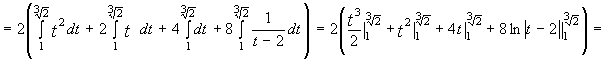
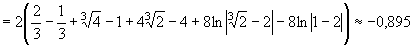
3)

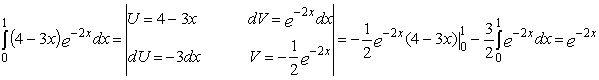
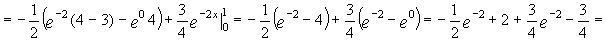
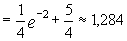
Несобственные интегралы.

В определении интеграла считается, что интервал интегрирования конечен и подынтегральная функция на нем ограничена. Если хотя бы одно из этих условий не выполнено, то интеграл называется несобственным.

Несобственным интегралом первого рода называется интеграл от ограниченной функции с бесконечными пределами интегрирования. За значение интеграла принимается предел, к которому стремится соответствующий определенны интеграл при стремлении пределов интегрирования к бесконечности:

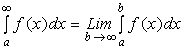
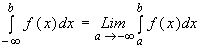
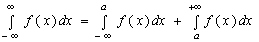
Если указанные пределы существуют (конечны), то говорят, что несобственный интеграл сходиться. Если же предел не существует или бесконечен, то говорят, что несобственный интеграл расходиться.

Если подынтегральная функция имеет на конечном отрезке интегрирования разрыв второго рода, то интеграл называется несобственным интегралом второго рода. В этом случае осуществляется обход точки разрыва с помощью предельного перехода.

Например, если функция f(x) определена и непрерывна на промежутке (a;b] и при x=a имеет особенность (либо не определена, либо имеет разрыв), то

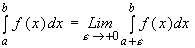
Если существует конечный предел, то говорят, что интеграл сходиться, в противном случае – расходиться.