Пусть функция 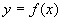 определена непрерывна и неотрицательна на отрезке
определена непрерывна и неотрицательна на отрезке 
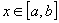 . Фигура, ограниченная графиком функции
. Фигура, ограниченная графиком функции 
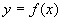 , осью абсцисс и прямыми х = а x = b (a < b), называется криволинейной трапецией. (рис.1)
, осью абсцисс и прямыми х = а x = b (a < b), называется криволинейной трапецией. (рис.1)
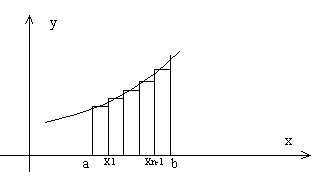
Рис.1.
Площадь криволинейной трапеции равна пределу, к которому стремится сумма площадей прямоугольников, на которые она распадается при разбиении отрезка [a,b] на частичные отрезки.
Таким образом, определенный интеграл функции 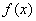 на отрезке [a,b] выражает площадь криволинейной трапеции.
на отрезке [a,b] выражает площадь криволинейной трапеции.
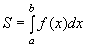
Если 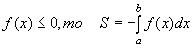
Чтобы найти площадь фигуры, заключенной между двумя кривыми 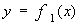 и
и 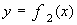 ,
, 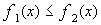 ,
, 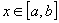 , надо рассмотреть разность площадей криволинейных трапеций, ограниченных графиками функций
, надо рассмотреть разность площадей криволинейных трапеций, ограниченных графиками функций 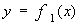 и
и 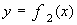 (рис.2)
(рис.2)
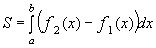
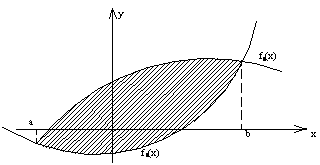
Рис.2
Пример. Вычислить площадь фигуры ограниченной линиями 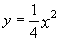 ,
, 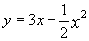
Решение. Для вычисления площади построим соответствующую фигуру, найдем точки пересечения кривых и воспользуемся нужной формулой.
Каждая из заданных кривых является параболой.
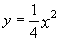 - парабола с вершиной в точке (0;0), ветви направлены вверх
- парабола с вершиной в точке (0;0), ветви направлены вверх
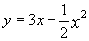 - парабола в вершиной в точке (3;4,5), ветви направлены вниз
- парабола в вершиной в точке (3;4,5), ветви направлены вниз
при 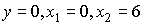
Точки пересечения кривых найдем из решения системы
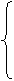
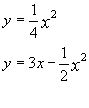
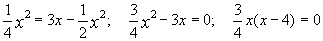
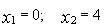
Выполним построение. (рис.3)
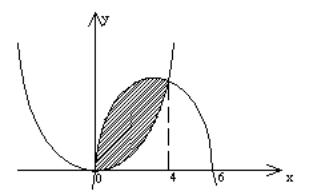
Рис.3
Воспользуемся формулой 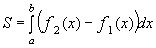 , где а = 0, b = 4,
, где а = 0, b = 4, 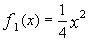 ,
, 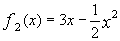
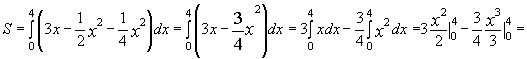
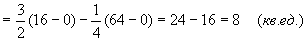
 2015-04-06
2015-04-06 418
418







