Определение. Линейным неоднородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
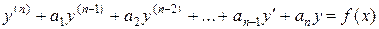 ,
,
где коэффициенты 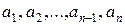 – заданные действительные числа, а
– заданные действительные числа, а  – заданная функция.
– заданная функция.
Метод решения. Согласно теореме 4.4 общим решением 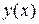 на отрезке
на отрезке  линейного неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами и непрерывной правой частью
линейного неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами и непрерывной правой частью  является сумма общего решения
является сумма общего решения
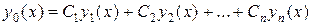
соответствующего однородного уравнения
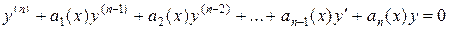
и какого-нибудь частного решения 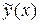 неоднородного уравнения:
неоднородного уравнения:
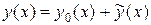 .
.
Общее решение однородного уравнения находить уже умеем, поэтому остается рассмотреть вопрос о нахождении частного решения 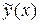 неоднородного уравнения.
неоднородного уравнения.
Если правая часть неоднородного уравнения, т.е. функция  – многочлен, либо показательная функция, либо тригонометрические функции
– многочлен, либо показательная функция, либо тригонометрические функции 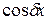 или
или 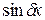 , либо линейная комбинация перечисленных функций, то частное решение
, либо линейная комбинация перечисленных функций, то частное решение 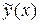 неоднородного уравнения может быть найдено методом неопределенных коэффициентов.
неоднородного уравнения может быть найдено методом неопределенных коэффициентов.
Если же правая часть неоднородного уравнения есть произвольная непрерывная функция, то частное решение 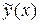 неоднородного уравнения может быть найдено методом вариации произвольных постоянных.
неоднородного уравнения может быть найдено методом вариации произвольных постоянных.
Рассмотрим оба перечисленных метода нахождения частного решения 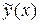 неоднородного уравнения.
неоднородного уравнения.
Метод неопределенных коэффициентов
Пусть правая часть неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид
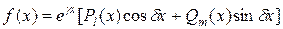 ,
,
где 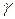 и
и 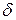 – действительные постоянные,
– действительные постоянные, 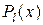 и
и 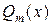 – многочлены от x соответственно l -й и m -й степени.
– многочлены от x соответственно l -й и m -й степени.
Тогда частное решение неоднородного уравнения ищем в виде
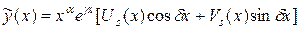 .
.
Здесь 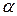 равно показателю кратности корня
равно показателю кратности корня 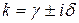 в характеристическом уравнении
в характеристическом уравнении
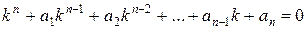 .
.
Если характеристическое уравнение такого корня не имеет, то следует положить 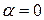 .
.
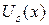 и
и 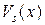 – полные (т.е. содержащие все степени x от 0 до s) многочлены от x степени s с неопределенными коэффициентами, причем s равно наибольшему из чисел l и m:
– полные (т.е. содержащие все степени x от 0 до s) многочлены от x степени s с неопределенными коэффициентами, причем s равно наибольшему из чисел l и m:
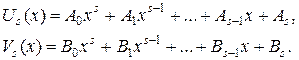
Если в выражение функции  входит хотя бы одна из функций
входит хотя бы одна из функций 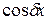 или
или 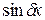 , то в решение
, то в решение 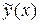 надо всегда вводить обе эти функции.
надо всегда вводить обе эти функции.
Неопределенные коэффициенты 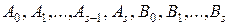 находятся из системы линейных алгебраических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного линейного неоднородного дифференциального уравнения после подстановки в него
находятся из системы линейных алгебраических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного линейного неоднородного дифференциального уравнения после подстановки в него 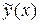 вместо y,
вместо y, 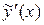 вместо
вместо 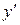 ,
, 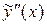 вместо
вместо 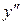 и т.д.
и т.д.
Если правая часть исходного дифференциального уравнения есть сумма нескольких функций рассматриваемой структуры:
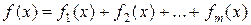 ,
,
и 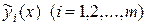 – соответствующие решения уравнений
– соответствующие решения уравнений
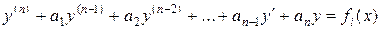 ,
,
то сумма
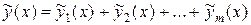 ,
,
как легко установить, является частным решением исходного уравнения (принцип наложения решений).
Пример. Найти общее решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
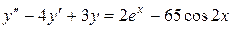 .
.
Решение данного неоднородного уравнения производится в три этапа.
1) Сначала находим общее решение соответствующего однородного уравнения:
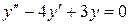
Для этого составляем и решаем характеристическое уравнение:
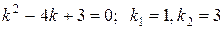 – два действительных простых корня.
– два действительных простых корня.
Частные решения однородного дифференциального уравнения:
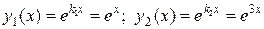 .
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
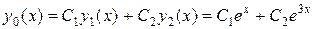 .
.
2) Далее ищем частное решение исходного неоднородного уравнения в виде
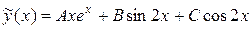 ,
,
так как характеристическое уравнение имеет корень 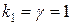
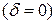 , а также согласно принципу наложения решений для правых частей
, а также согласно принципу наложения решений для правых частей 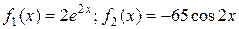 .
.
Для определения коэффициентов 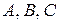 находим производные
находим производные 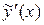 и
и 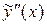 :
:
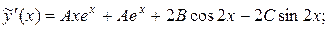
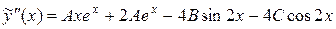
и подставляем их в исходное неоднородное уравнение:
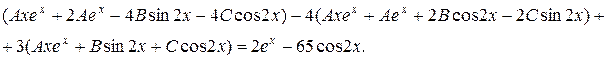 Раскроем скобки и приведем подобные в левой части равенства:
Раскроем скобки и приведем подобные в левой части равенства:
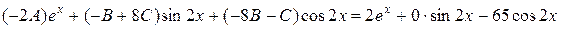 .
.
Приравнивая коэффициенты у подобных членов из обеих частей равенства, получим систему уравнений для определения коэффициентов 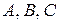 и найдем их значения:
и найдем их значения:
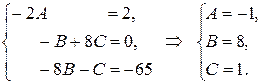
Таким образом, частное решение неоднородного уравнения имеет вид:
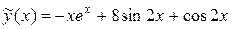 .
.
3) Общее решение исходного неоднородного дифференциального уравнения найдем как сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения:
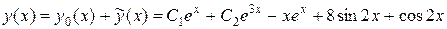 .
.
Метод вариации произвольных постоянных (метод Лагранжа)
Частное решение линейного неоднородного дифференциального уравнения
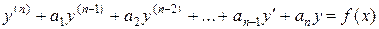
можно найти методом вариации произвольных постоянных, если известно общее решение
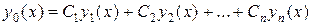
соответствующего однородного уравнения
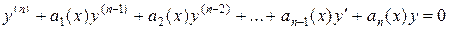 .
.
Именно, будем искать частное решение неоднородного уравнения в виде
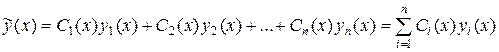 ,
,
где 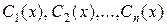 – неизвестные функции, для определения которых нужно составить n уравнений.
– неизвестные функции, для определения которых нужно составить n уравнений.
Найдем 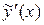 :
:
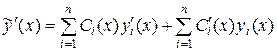 .
.
Положив
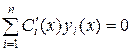 ,
,
получим первое из n искомых уравнений.
Найдем 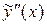 :
:
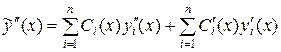 .
.
Положив
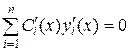 ,
,
получим второе из n искомых уравнений.
Продолжая аналогичным образом, найдем 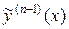 :
:
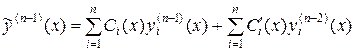 .
.
Положив
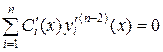 ,
,
получим 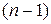 -е из n искомых уравнений.
-е из n искомых уравнений.
Найдем 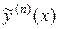 :
:
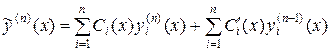
и, подставив в исходное неоднородное уравнение 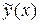 вместо y,
вместо y, 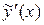 вместо
вместо 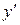 ,
, 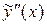 вместо
вместо 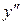 ,…,
,…, 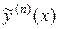 вместо
вместо 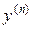 , получим последнее n -е из n искомых уравнений для определения n неизвестных функций
, получим последнее n -е из n искомых уравнений для определения n неизвестных функций 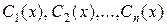 :
:
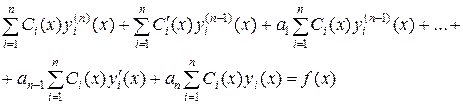
или
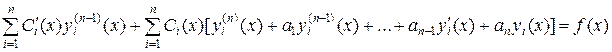 ,
,
или
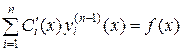 ,
,
так как 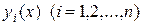 – решения однородного уравнения
– решения однородного уравнения
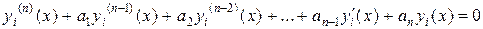 .
.
Таким образом, получили систему из n линейных неоднородных алгебраических уравнений для определения производных от n неизвестных функций 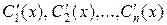 :
:
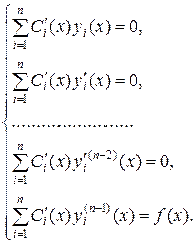
Примем без доказательства, что определитель системы отличен от нуля. Тогда система имеет единственное решение 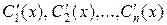 . Определив все
. Определив все 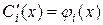 , после интегрирования получаем
, после интегрирования получаем
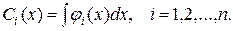 ,
,
Следовательно, частное решение исходного линейного неоднородного дифференциального уравнения имеет вид
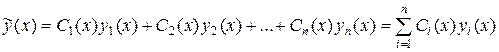 ,
,
где функции 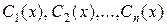 определяются полученными равенствами, а
определяются полученными равенствами, а 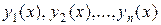 – известные линейно независимые частные решения соответствующего однородного уравнения.
– известные линейно независимые частные решения соответствующего однородного уравнения.
Пример. Найти частное решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
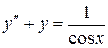 .
.
1) Сначала находим общее решение соответствующего однородного уравнения
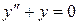 .
.
Для этого составляем и решаем характеристическое уравнение:
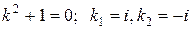 – пара комплексно сопряженных простых корней
– пара комплексно сопряженных простых корней 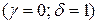 .
.
Частные решения соответствующего однородного дифференциального уравнения:
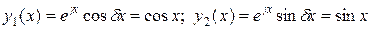 .
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
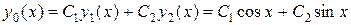 .
.
2) Далее ищем частное решение исходного неоднородного дифференциального уравнения в виде
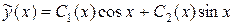 .
.
Составляем и решаем систему неоднородных алгебраических уравнений для определения 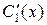 и
и 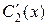 :
:
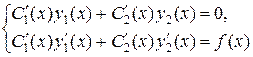
или
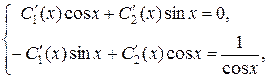
откуда находим
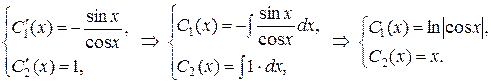
Таким образом, частное решение исходного неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами имеет вид
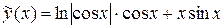 .
.
 2015-04-23
2015-04-23 8821
8821
