Третье уравнение Максвелла базируется на законе Гаусса, который связывает поток вектора электрической индукции через произвольную замкнутую поверхность с зарядом, сосредоточенным внутри этой поверхности:
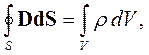 | (2.12) |
| где | S - произвольная замкнутая поверхность, |
| dS - векторный дифференциал поверхности:dS = n0dS, | |
| n0 - орт внешней нормали к поверхности S, | |
| V – объем, ограниченный поверхностью S, | |
| ρ – объемная плотность заряда внутри поверхности S. |
Гаусс получил уравнение (2.12) применительно к постоянным полям. Максвелл предположил, что его можно использовать и в случае переменных полей. Поэтому уравнение (2.12) обычно называют третьим уравнением Максвелла в интегральной форме.
Для перехода к дифференциальной форме надо преобразовать левую часть уравнения (2.12) по теореме Остроградского – Гаусса (формула (1.33) [6]). Получим:
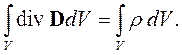 | (2.13) |
Так как никаких ограничений на объем V не наложено, равенство (2.13) выполнится только в том случае, если равны подынтегральные выражения:
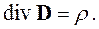 | (2.14) |
Это соотношение называется третьим уравнением Максвелла в дифференциальной форме.
В декартовой системе координат можно от векторного уравнения перейти к скалярному:
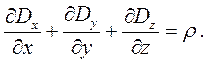 | (2.15) |
Из равенства (2.14) следует, что дивергенция вектора электрической индукции отлична от нуля только в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора электрической индукции начинаются на положительных зарядах и заканчиваются на отрицательных.
 2015-04-01
2015-04-01 4814
4814
