Вычисляя на основании имеющихся у нас выборочных данных оценку 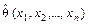 параметра q, мы понимаем, что величина
параметра q, мы понимаем, что величина 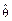 является лишь приближенным значением неизвестного параметра q, даже в том случае, когда эта оценка состоятельна, несмещённа и эффективна. Поэтому возникает вопрос: как сильно отклоняется это приближенное значение от истинного? Нельзя ли указать интервал вида
является лишь приближенным значением неизвестного параметра q, даже в том случае, когда эта оценка состоятельна, несмещённа и эффективна. Поэтому возникает вопрос: как сильно отклоняется это приближенное значение от истинного? Нельзя ли указать интервал вида 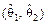 , который с заранее заданной вероятностью, близкой к единице, накрывает неизвестное нам истинное значение q искомого параметра?
, который с заранее заданной вероятностью, близкой к единице, накрывает неизвестное нам истинное значение q искомого параметра?
Если такой интервал мы сможем построить, то длина интервала 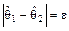 ,
, 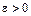 будет характеризовать точность вычисления оценки параметра q: чем меньше величина
будет характеризовать точность вычисления оценки параметра q: чем меньше величина 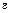 , тем точнее оценка. Действительно, если случайный интервал
, тем точнее оценка. Действительно, если случайный интервал 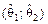 накрывает с заданной вероятностью истинное значение параметра q, то, принимая за оценку параметра q значение
накрывает с заданной вероятностью истинное значение параметра q, то, принимая за оценку параметра q значение 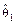 (или
(или 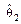 ), мы допустим ошибку не более, чем
), мы допустим ошибку не более, чем 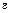 .
.
Доверительной вероятностью оценки называется вероятность 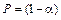 выполнения неравенства
выполнения неравенства 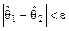 :
: 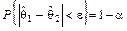 ;
; 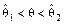 . Выбор доверительной вероятности определяется конкретными условиями; обычно используются значения
. Выбор доверительной вероятности определяется конкретными условиями; обычно используются значения 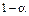 , равные 0,90; 0,95; 0,99.
, равные 0,90; 0,95; 0,99.
Доверительная вероятность оценки показывает, что при извлечении достаточно большого числа выборок объема n из одной и той же генеральной совокупности с функцией распределения F (x, q) в 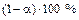 случаях параметр q будет накрываться интервалом
случаях параметр q будет накрываться интервалом 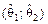 , и лишь
, и лишь 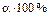 интервалов
интервалов 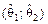 не содержит оцениваемый параметр.
не содержит оцениваемый параметр.
Доверительным интервалом называется интервал 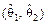 , накрывающий неизвестный параметр q с заданной доверительной вероятностью
, накрывающий неизвестный параметр q с заданной доверительной вероятностью 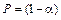 .
.
Мы говорим «Интервал 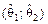 будет накрывать неизвестное истинное значение параметра q» потому, что значение
будет накрывать неизвестное истинное значение параметра q» потому, что значение 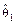 и
и 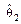 вычисляются по выборке и поэтому случайны и изменяют свои значения от выборки к выборке, а значение параметра q остается неизменным.
вычисляются по выборке и поэтому случайны и изменяют свои значения от выборки к выборке, а значение параметра q остается неизменным.
Иногда удается построить доверительный интервал, границы которого симметричны относительно точечной оценки 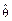 параметра
параметра 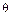 :
: 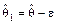 ;
; 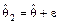 . И тогда
. И тогда 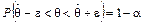 или
или 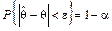 .
.
 2015-04-08
2015-04-08 740
740








